Menu Close

Find-all-integers-n-such-that-n-2-n-1-n-2-1-

Tinku Tara 0 Comments
Pin




Question Number 17454 by Tinkutara last updated on 06/Jul/17
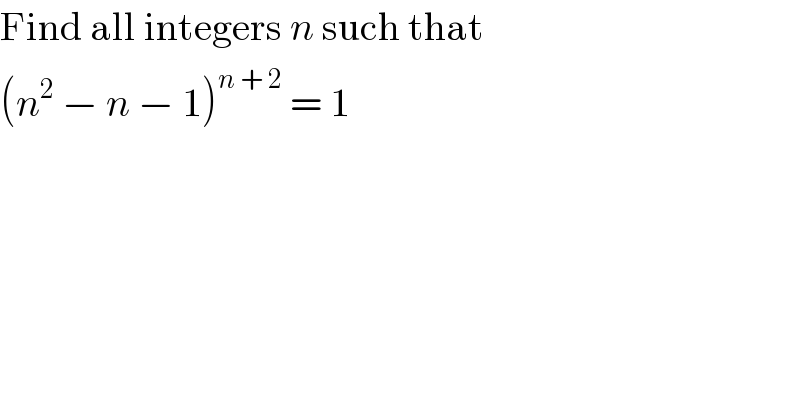
Find all integers n such that (n^2 − n − 1)^(n + 2) = 1
Findallintegersnsuchthat(n2−n−1)n+2=1
Answered by mrW1 last updated on 06/Jul/17
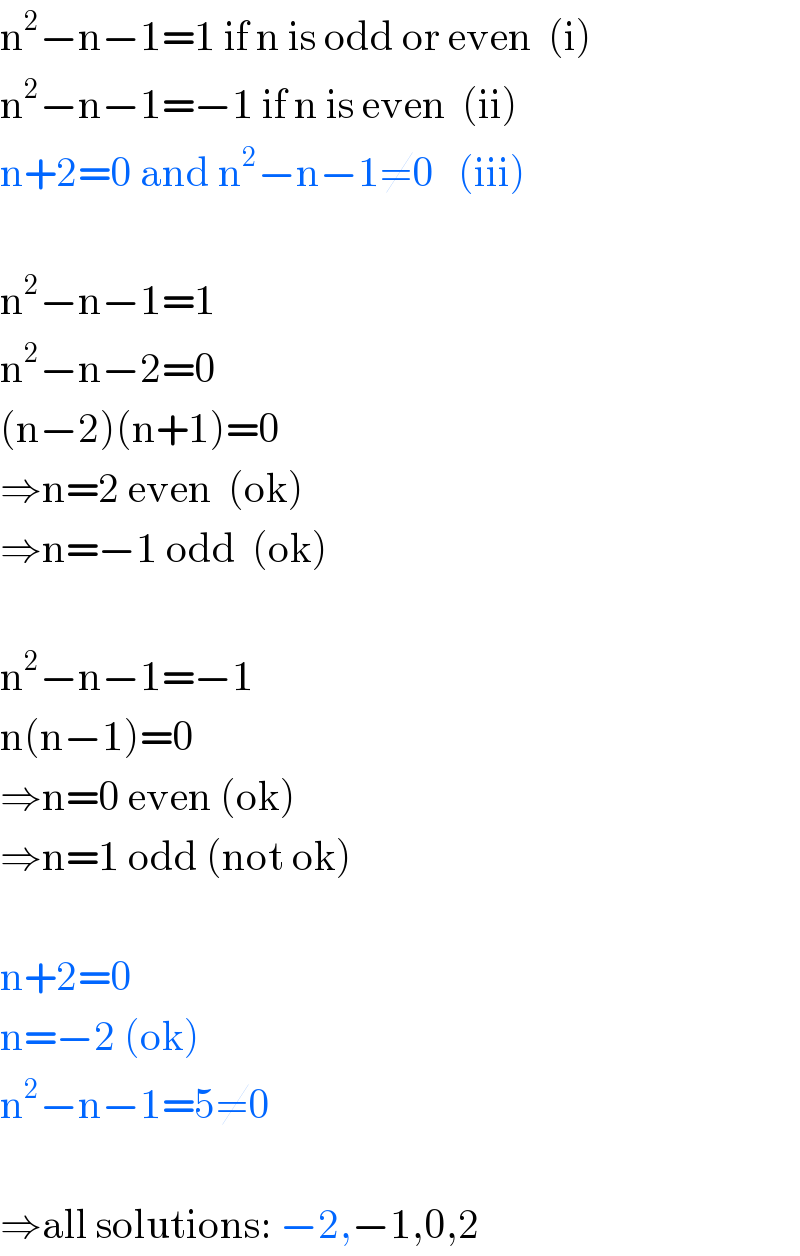
n^2 −n−1=1 if n is odd or even (i) n^2 −n−1=−1 if n is even (ii) n+2=0 and n^2 −n−1≠0 (iii) n^2 −n−1=1 n^2 −n−2=0 (n−2)(n+1)=0 ⇒n=2 even (ok) ⇒n=−1 odd (ok) n^2 −n−1=−1 n(n−1)=0 ⇒n=0 even (ok) ⇒n=1 odd (not ok) n+2=0 n=−2 (ok) n^2 −n−1=5≠0 ⇒all solutions: −2,−1,0,2
n2−n−1=1ifnisoddoreven(i)n2−n−1=−1ifniseven(ii)n+2=0andn2−n−1≠0(iii)n2−n−1=1n2−n−2=0(n−2)(n+1)=0⇒n=2even(ok)⇒n=−1odd(ok)n2−n−1=−1n(n−1)=0⇒n=0even(ok)⇒n=1odd(notok)n+2=0n=−2(ok)n2−n−1=5≠0⇒allsolutions:−2,−1,0,2
Commented by Tinkutara last updated on 06/Jul/17
Thanks Sir!
ThanksSir!
Commented by RasheedSoomro last updated on 06/Jul/17
Also n=−2
Alson=−2
Commented by mrW1 last updated on 06/Jul/17
you are right sir!
youarerightsir!
Commented by RasheedSoomro last updated on 09/Jul/17
G ⊚^(⌢) ⊚^(⌢) _(⌣) D approach!
G⊚⌢⌣⊚⌢Dapproach!

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *