find-all-numbers-gt-1-from-N-which-their-cube-are-lt-18360-

Question Number 118181 by mathocean1 last updated on 15/Oct/20

f i n d a l l n u m b e r s > 1 f r o m N w h i c h

t h e i r c u b e a r e < 18360

Commented by mathocean1 last updated on 15/Oct/20

t h a n k s

Answered by TANMAY PANACEA last updated on 15/Oct/20

18360 = 3 \times 6120

= 3 \times 3 \times 2040

= 3^{3} \times 680

= 3^{3} \times 2^{3} \times 85

3^{3} \times 2^{3} \times 4^{3} < 3^{3} \times 2^{3} \times 85 < 3^{3} \times 2^{3} \times 5^{3}

s o t h e n u m b e r s a r e

2^{3} = 8

3^{3} = 27

4^{3} = 64

2^{3} \times 3^{3} = 216

2^{3} \times 4^{3} = 512

3^{3} \times 4^{3} = 144 \times 12 = 1728

2^{3} \times 3^{3} \times 4^{3} = 13824

s o r e q u i r e d a n s w e r

{2, 3, 4, 6, 8, 12, 24}

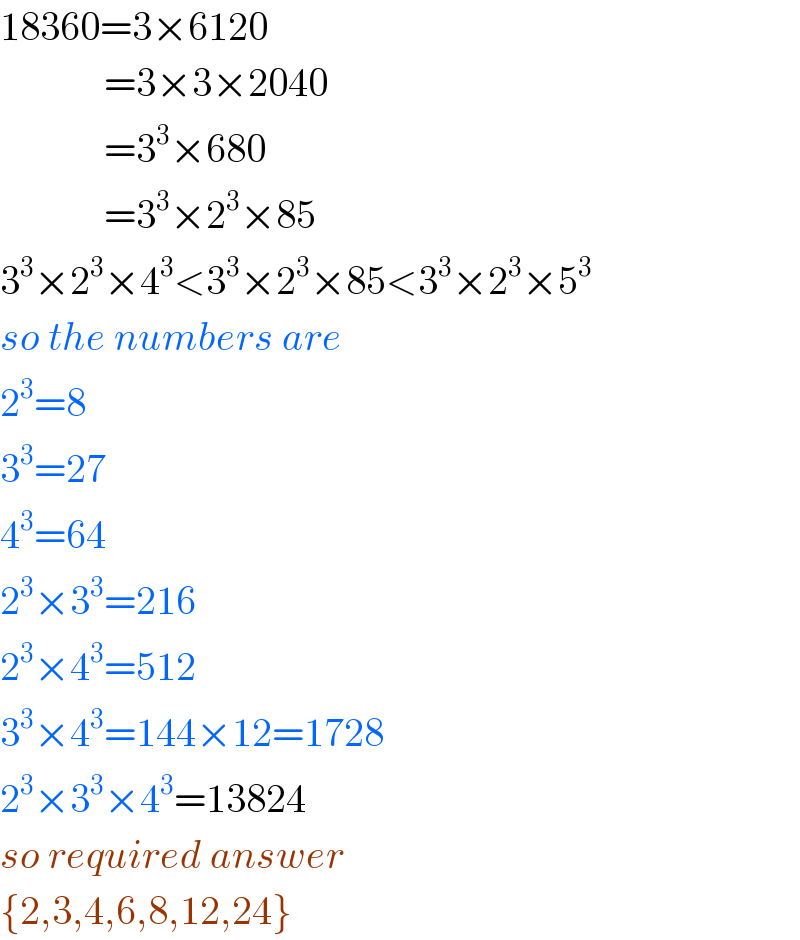
Commented by mathocean1 last updated on 15/Oct/20

t h a n k s

Commented by mr W last updated on 15/Oct/20

27^{3} = 19683 > 18360

26^{3} = 17576 < 18360 ✓

\Rightarrow 2 ⩽ n ⩽ 26

Facebook Tweet Pin