Menu Close

Find-all-pair-x-y-of-real-numbers-that-are-the-solutions-to-the-system-x-4-2x-3-y-1-4-3-y-4-2y-3-x-1-4-3-

Tinku Tara 0 Comments
Pin




Question Number 119849 by benjo_mathlover last updated on 27/Oct/20
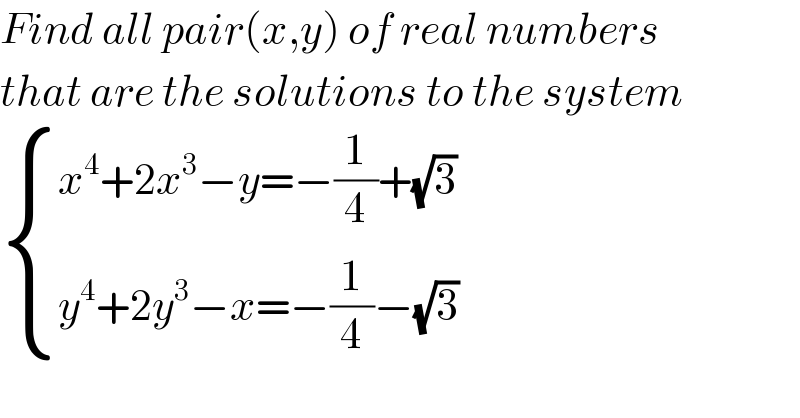
Find all pair(x,y) of real numbers that are the solutions to the system { ((x^4 +2x^3 −y=−(1/4)+(√3))),((y^4 +2y^3 −x=−(1/4)−(√3))) :}
$${Find}\:{all}\:{pair}\left({x},{y}\right)\:{of}\:{real}\:{numbers} \\ $$$${that}\:{are}\:{the}\:{solutions}\:{to}\:{the}\:{system} \\ $$$$\begin{cases}{{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} −{y}=−\frac{\mathrm{1}}{\mathrm{4}}+\sqrt{\mathrm{3}}}\\{{y}^{\mathrm{4}} +\mathrm{2}{y}^{\mathrm{3}} −{x}=−\frac{\mathrm{1}}{\mathrm{4}}−\sqrt{\mathrm{3}}}\end{cases} \\ $$
Answered by 1549442205PVT last updated on 27/Oct/20
Adding up two the equations we get x^4 +2x^3 −y+(1/4)+y^4 +2y^3 −x+(1/4)=0 ⇔(x^2 +x−(1/2))^2 +(y^2 +y−(1/2))^2 =0 ⇔ { ((x^2 +x−(1/2)=0)),((y^2 +y−(1/2)=0)) :} Δ=1+4.0.5=3,so x= { ((x=((−1±(√3))/2))),((y=((−1±(√3))/2))) :} Thus the solutions of given system are (x,y)∈{(((−1−(√3))/2),((−1−(√3))/2)),(((−1−(√3))/2),((−1+(√3))/2)) ,(((−1+(√3))/2),((−1−(√3))/2)),(((−1+(√3))/2),((−1+(√3))/2))}
$$\mathrm{Adding}\:\mathrm{up}\:\mathrm{two}\:\mathrm{the}\:\mathrm{equations}\:\mathrm{we}\:\mathrm{get} \\ $$$${x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{3}} −{y}+\frac{\mathrm{1}}{\mathrm{4}}+{y}^{\mathrm{4}} +\mathrm{2}{y}^{\mathrm{3}} −{x}+\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\mathrm{y}^{\mathrm{2}} +\mathrm{y}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Leftrightarrow\begin{cases}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0}}\\{\mathrm{y}^{\mathrm{2}} +\mathrm{y}−\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0}}\end{cases} \\ $$$$\Delta=\mathrm{1}+\mathrm{4}.\mathrm{0}.\mathrm{5}=\mathrm{3},\mathrm{so}\:\mathrm{x}=\begin{cases}{\mathrm{x}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{3}}}{\mathrm{2}}}\\{\mathrm{y}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{3}}}{\mathrm{2}}}\end{cases} \\ $$$$\mathrm{Thus}\:\mathrm{the}\:\mathrm{solutions}\:\mathrm{of}\:\mathrm{given}\:\mathrm{system}\:\mathrm{are} \\ $$$$\left(\mathrm{x},\mathrm{y}\right)\in\left\{\left(\frac{−\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{2}},\frac{−\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{2}}\right),\left(\frac{−\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{2}},\frac{−\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\right. \\ $$$$\left.,\left(\frac{−\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{2}},\frac{−\mathrm{1}−\sqrt{\mathrm{3}}}{\mathrm{2}}\right),\left(\frac{−\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{2}},\frac{−\mathrm{1}+\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\right\} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *