Question Number 115906 by Eric002 last updated on 29/Sep/20
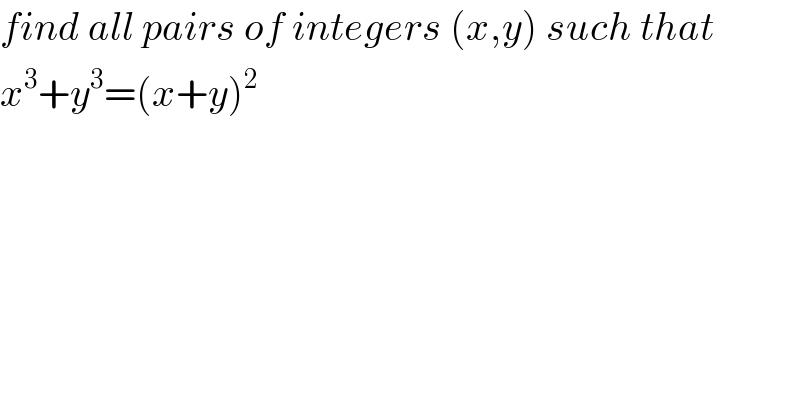
$${find}\:{all}\:{pairs}\:{of}\:{integers}\:\left({x},{y}\right)\:{such}\:{that} \\ $$$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} =\left({x}+{y}\right)^{\mathrm{2}} \\ $$
Answered by mindispower last updated on 29/Sep/20
![x^3 +y^3 =(x+y)(x^2 +y^2 −xy) ⇔(x+y)(x^2 +y^2 −xy−(x+y))=0 x=−y or x^2 +y^2 −xy−(x+y)=0 y^2 +y(−1−x)+x^2 −x=0 Δ=x^2 +2x+1−4x^2 +4x≥0 ⇒6x−4x^2 +1≥0 x∈[((−6+(√(48)))/(−8)),((6+(√(48)))/8)] 0≤x≤1 x=0⇒y^2 −y=0⇒y∈{0,1} x=1⇒y^2 −2y=0 y∈{0,2} S={(a,−a);(0,1);(0,2)}](https://www.tinkutara.com/question/Q115911.png)
$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} =\left({x}+{y}\right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} −{xy}\right) \\ $$$$\Leftrightarrow\left({x}+{y}\right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} −{xy}−\left({x}+{y}\right)\right)=\mathrm{0} \\ $$$${x}=−{y} \\ $$$${or} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −{xy}−\left({x}+{y}\right)=\mathrm{0} \\ $$$${y}^{\mathrm{2}} +{y}\left(−\mathrm{1}−{x}\right)+{x}^{\mathrm{2}} −{x}=\mathrm{0} \\ $$$$\Delta={x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}−\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{x}\geqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{6}{x}−\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}\geqslant\mathrm{0} \\ $$$${x}\in\left[\frac{−\mathrm{6}+\sqrt{\mathrm{48}}}{−\mathrm{8}},\frac{\mathrm{6}+\sqrt{\mathrm{48}}}{\mathrm{8}}\right] \\ $$$$\:\mathrm{0}\leqslant{x}\leqslant\mathrm{1} \\ $$$${x}=\mathrm{0}\Rightarrow{y}^{\mathrm{2}} −{y}=\mathrm{0}\Rightarrow{y}\in\left\{\mathrm{0},\mathrm{1}\right\} \\ $$$${x}=\mathrm{1}\Rightarrow{y}^{\mathrm{2}} −\mathrm{2}{y}=\mathrm{0} \\ $$$${y}\in\left\{\mathrm{0},\mathrm{2}\right\} \\ $$$${S}=\left\{\left({a},−{a}\right);\left(\mathrm{0},\mathrm{1}\right);\left(\mathrm{0},\mathrm{2}\right)\right\} \\ $$
