Find-all-real-solutions-of-x-y-such-that-x-3y-4-x-y-5-y-3x-5-x-y-7-

Question Number 83756 by naka3546 last updated on 05/Mar/20

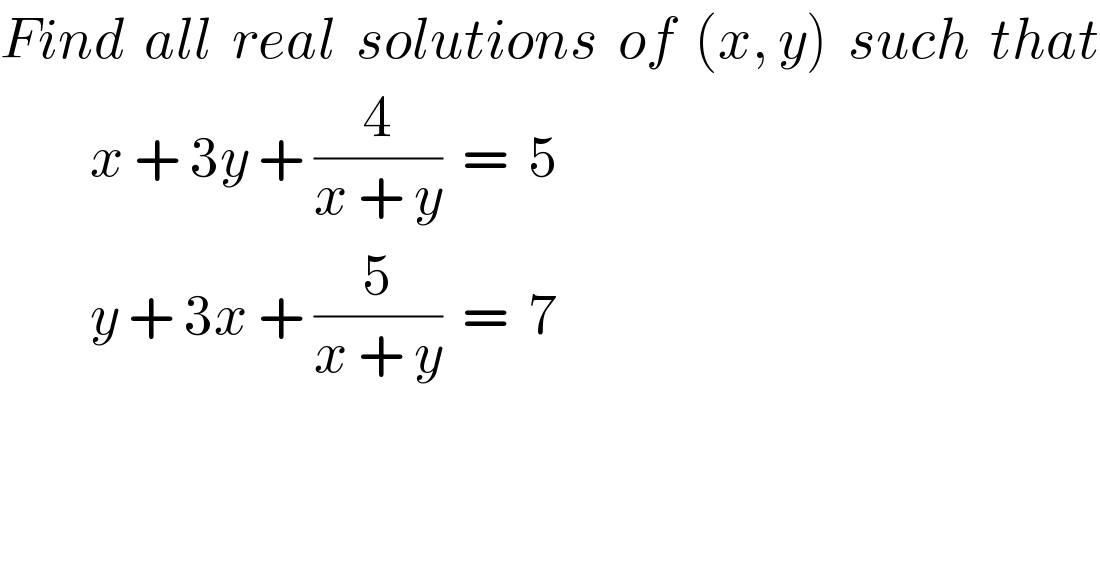
F i n d a l l r e a l s o l u t i o n s o f (x, y) s u c h t h a t

x + 3 y + \frac{4}{x + y} = 5

y + 3 x + \frac{5}{x + y} = 7

Commented by Prithwish Sen 1 last updated on 05/Mar/20

adding both

4 (x + y) + \frac{9}{(x + y)} = 12

{4 a}^{2} - 12 a + 9 = 0 putting x + y = a

a = \frac{3}{2} \Rightarrow x + y = \frac{3}{2} \dots (i)

substracting

2 (x - y) + \frac{1}{x + y} = 2

x - y = \frac{2}{3} \dots . (ii)

from (i) and (ii) we get

x = \frac{13}{12} and y = \frac{5}{12}

please check

Commented by naka3546 last updated on 06/Mar/20

t h a n k y o u, s i r .

Commented by Prithwish Sen 1 last updated on 06/Mar/20

welcome