Question Number 57997 by peter frank last updated on 15/Apr/19
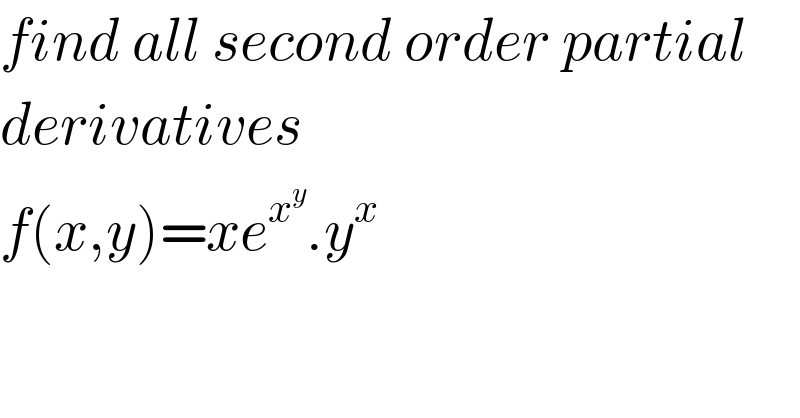
$${find}\:{all}\:{second}\:{order}\:{partial} \\ $$$${derivatives} \\ $$$${f}\left({x},{y}\right)={xe}^{{x}^{{y}} } .{y}^{{x}} \\ $$
Commented by MJS last updated on 16/Apr/19
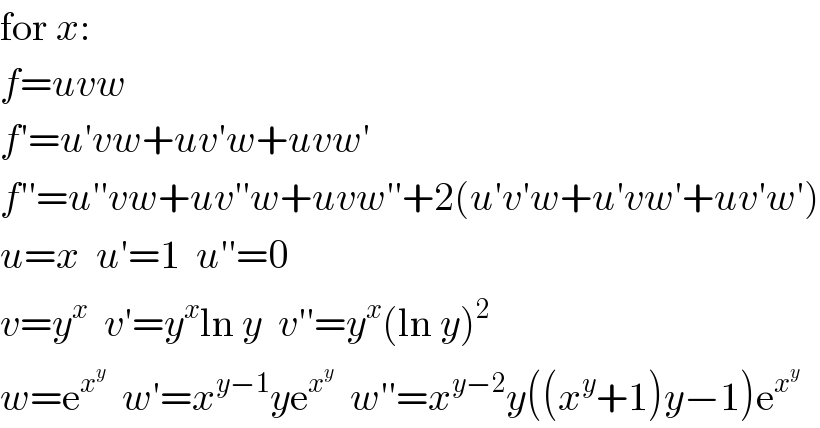
$$\mathrm{for}\:{x}: \\ $$$${f}={uvw} \\ $$$${f}'={u}'{vw}+{uv}'{w}+{uvw}' \\ $$$${f}''={u}''{vw}+{uv}''{w}+{uvw}''+\mathrm{2}\left({u}'{v}'{w}+{u}'{vw}'+{uv}'{w}'\right) \\ $$$${u}={x}\:\:{u}'=\mathrm{1}\:\:{u}''=\mathrm{0} \\ $$$${v}={y}^{{x}} \:\:{v}'={y}^{{x}} \mathrm{ln}\:{y}\:\:{v}''={y}^{{x}} \left(\mathrm{ln}\:{y}\right)^{\mathrm{2}} \\ $$$${w}=\mathrm{e}^{{x}^{{y}} } \:\:{w}'={x}^{{y}−\mathrm{1}} {y}\mathrm{e}^{{x}^{{y}} } \:\:{w}''={x}^{{y}−\mathrm{2}} {y}\left(\left({x}^{{y}} +\mathrm{1}\right){y}−\mathrm{1}\right)\mathrm{e}^{{x}^{{y}} } \\ $$
Commented by MJS last updated on 16/Apr/19
is it an imposition for bad behavior? ��
