Question Number 126005 by bramlexs22 last updated on 16/Dec/20
![Find all solution 7cos (3x)−1= 3 for x over the interval [ 0,2π ]](https://www.tinkutara.com/question/Q126005.png)
$$\:\:{Find}\:{all}\:{solution}\:\mathrm{7cos}\:\left(\mathrm{3}{x}\right)−\mathrm{1}=\:\mathrm{3}\: \\ $$$${for}\:{x}\:{over}\:{the}\:{interval}\:\left[\:\mathrm{0},\mathrm{2}\pi\:\right]\: \\ $$
Commented by liberty last updated on 16/Dec/20
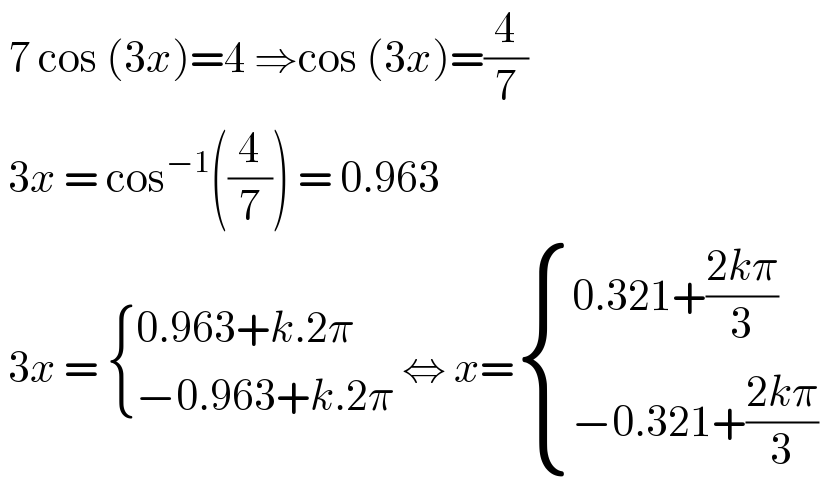
$$\:\mathrm{7}\:\mathrm{cos}\:\left(\mathrm{3}{x}\right)=\mathrm{4}\:\Rightarrow\mathrm{cos}\:\left(\mathrm{3}{x}\right)=\frac{\mathrm{4}}{\mathrm{7}}\: \\ $$$$\:\mathrm{3}{x}\:=\:\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{4}}{\mathrm{7}}\right)\:=\:\mathrm{0}.\mathrm{963} \\ $$$$\:\mathrm{3}{x}\:=\:\begin{cases}{\mathrm{0}.\mathrm{963}+{k}.\mathrm{2}\pi}\\{−\mathrm{0}.\mathrm{963}+{k}.\mathrm{2}\pi}\end{cases}\:\Leftrightarrow\:{x}=\begin{cases}{\mathrm{0}.\mathrm{321}+\frac{\mathrm{2}{k}\pi}{\mathrm{3}}}\\{−\mathrm{0}.\mathrm{321}+\frac{\mathrm{2}{k}\pi}{\mathrm{3}}}\end{cases} \\ $$
