Question Number 61923 by naka3546 last updated on 12/Jun/19
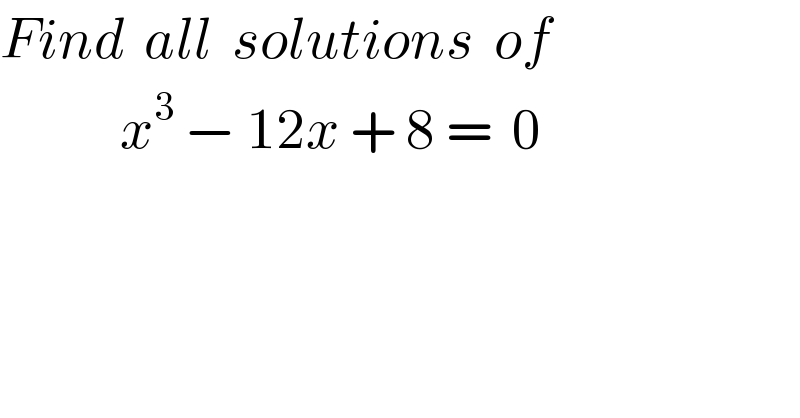
$${Find}\:\:{all}\:\:{solutions}\:\:{of} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{3}} \:−\:\mathrm{12}{x}\:+\:\mathrm{8}\:=\:\:\mathrm{0} \\ $$
Answered by MJS last updated on 12/Jun/19

$${x}^{\mathrm{3}} +{px}+{q}=\mathrm{0} \\ $$$$ \\ $$$${p}=−\mathrm{12} \\ $$$${q}=\mathrm{8} \\ $$$${D}=\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}=−\mathrm{48}<\mathrm{0}\:\Rightarrow\:\mathrm{trigonometric}\:\mathrm{method} \\ $$$${x}_{{k}} =\frac{\mathrm{2}\sqrt{−\mathrm{3}{p}}}{\mathrm{3}}\mathrm{sin}\:\left(\frac{\mathrm{2}\pi{k}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\mathrm{3}\sqrt{\mathrm{3}}{q}}{\mathrm{2}\sqrt{−{p}^{\mathrm{3}} }}\right)\:\mathrm{with}\:{k}=\mathrm{0},\:\mathrm{1},\:\mathrm{2} \\ $$$${x}_{\mathrm{0}} =\mathrm{4sin}\:\frac{\pi}{\mathrm{18}} \\ $$$${x}_{\mathrm{1}} =\mathrm{4cos}\:\frac{\mathrm{2}\pi}{\mathrm{9}} \\ $$$${x}_{\mathrm{2}} =−\mathrm{4cos}\:\frac{\pi}{\mathrm{9}} \\ $$
