Menu Close

Find-all-the-real-solutions-of-cos-x-cos-5-x-cos-7x-3-

Tinku Tara 0 Comments
Pin




Question Number 150871 by liberty last updated on 16/Aug/21
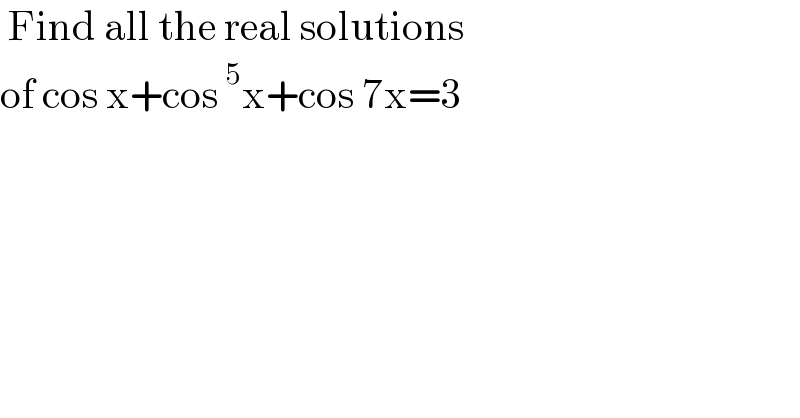
Find all the real solutions of cos x+cos^5 x+cos 7x=3
$$\:\mathrm{Find}\:\mathrm{all}\:\mathrm{the}\:\mathrm{real}\:\mathrm{solutions} \\ $$$$\mathrm{of}\:\mathrm{cos}\:\mathrm{x}+\mathrm{cos}\:^{\mathrm{5}} \mathrm{x}+\mathrm{cos}\:\mathrm{7x}=\mathrm{3} \\ $$
Answered by EDWIN88 last updated on 16/Aug/21
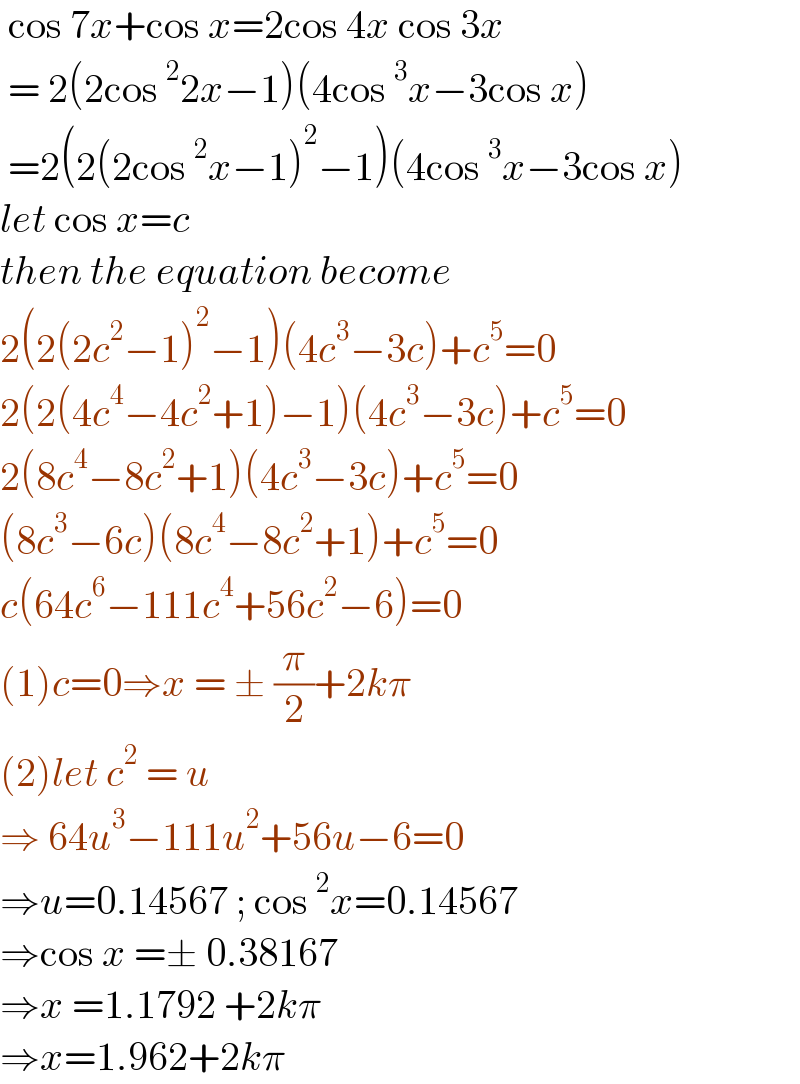
cos 7x+cos x=2cos 4x cos 3x = 2(2cos^2 2x−1)(4cos^3 x−3cos x) =2(2(2cos^2 x−1)^2 −1)(4cos^3 x−3cos x) let cos x=c then the equation become 2(2(2c^2 −1)^2 −1)(4c^3 −3c)+c^5 =0 2(2(4c^4 −4c^2 +1)−1)(4c^3 −3c)+c^5 =0 2(8c^4 −8c^2 +1)(4c^3 −3c)+c^5 =0 (8c^3 −6c)(8c^4 −8c^2 +1)+c^5 =0 c(64c^6 −111c^4 +56c^2 −6)=0 (1)c=0⇒x = ± (π/2)+2kπ (2)let c^2 = u ⇒ 64u^3 −111u^2 +56u−6=0 ⇒u=0.14567 ; cos^2 x=0.14567 ⇒cos x =± 0.38167 ⇒x =1.1792 +2kπ ⇒x=1.962+2kπ
$$\:\mathrm{cos}\:\mathrm{7}{x}+\mathrm{cos}\:{x}=\mathrm{2cos}\:\mathrm{4}{x}\:\mathrm{cos}\:\mathrm{3}{x} \\ $$$$\:=\:\mathrm{2}\left(\mathrm{2cos}\:^{\mathrm{2}} \mathrm{2}{x}−\mathrm{1}\right)\left(\mathrm{4cos}\:^{\mathrm{3}} {x}−\mathrm{3cos}\:{x}\right) \\ $$$$\:=\mathrm{2}\left(\mathrm{2}\left(\mathrm{2cos}\:^{\mathrm{2}} {x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{4cos}\:^{\mathrm{3}} {x}−\mathrm{3cos}\:{x}\right) \\ $$$${let}\:\mathrm{cos}\:{x}={c}\: \\ $$$${then}\:{the}\:{equation}\:{become} \\ $$$$\mathrm{2}\left(\mathrm{2}\left(\mathrm{2}{c}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{4}{c}^{\mathrm{3}} −\mathrm{3}{c}\right)+{c}^{\mathrm{5}} =\mathrm{0} \\ $$$$\mathrm{2}\left(\mathrm{2}\left(\mathrm{4}{c}^{\mathrm{4}} −\mathrm{4}{c}^{\mathrm{2}} +\mathrm{1}\right)−\mathrm{1}\right)\left(\mathrm{4}{c}^{\mathrm{3}} −\mathrm{3}{c}\right)+{c}^{\mathrm{5}} =\mathrm{0} \\ $$$$\mathrm{2}\left(\mathrm{8}{c}^{\mathrm{4}} −\mathrm{8}{c}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{4}{c}^{\mathrm{3}} −\mathrm{3}{c}\right)+{c}^{\mathrm{5}} =\mathrm{0} \\ $$$$\left(\mathrm{8}{c}^{\mathrm{3}} −\mathrm{6}{c}\right)\left(\mathrm{8}{c}^{\mathrm{4}} −\mathrm{8}{c}^{\mathrm{2}} +\mathrm{1}\right)+{c}^{\mathrm{5}} =\mathrm{0} \\ $$$${c}\left(\mathrm{64}{c}^{\mathrm{6}} −\mathrm{111}{c}^{\mathrm{4}} +\mathrm{56}{c}^{\mathrm{2}} −\mathrm{6}\right)=\mathrm{0} \\ $$$$\left(\mathrm{1}\right){c}=\mathrm{0}\Rightarrow{x}\:=\:\pm\:\frac{\pi}{\mathrm{2}}+\mathrm{2}{k}\pi \\ $$$$\left(\mathrm{2}\right){let}\:{c}^{\mathrm{2}} \:=\:{u}\: \\ $$$$\Rightarrow\:\mathrm{64}{u}^{\mathrm{3}} −\mathrm{111}{u}^{\mathrm{2}} +\mathrm{56}{u}−\mathrm{6}=\mathrm{0} \\ $$$$\Rightarrow{u}=\mathrm{0}.\mathrm{14567}\:;\:\mathrm{cos}\:^{\mathrm{2}} {x}=\mathrm{0}.\mathrm{14567} \\ $$$$\Rightarrow\mathrm{cos}\:{x}\:=\pm\:\mathrm{0}.\mathrm{38167} \\ $$$$\Rightarrow{x}\:=\mathrm{1}.\mathrm{1792}\:+\mathrm{2}{k}\pi \\ $$$$\Rightarrow{x}=\mathrm{1}.\mathrm{962}+\mathrm{2}{k}\pi \\ $$
Commented by MJS_new last updated on 16/Aug/21
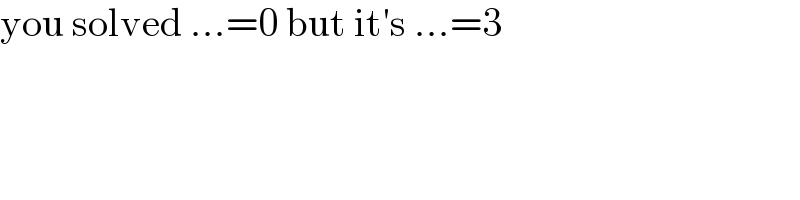
you solved ...=0 but it′s ...=3
$$\mathrm{you}\:\mathrm{solved}\:…=\mathrm{0}\:\mathrm{but}\:\mathrm{it}'\mathrm{s}\:…=\mathrm{3} \\ $$
Commented by john_santu last updated on 16/Aug/21
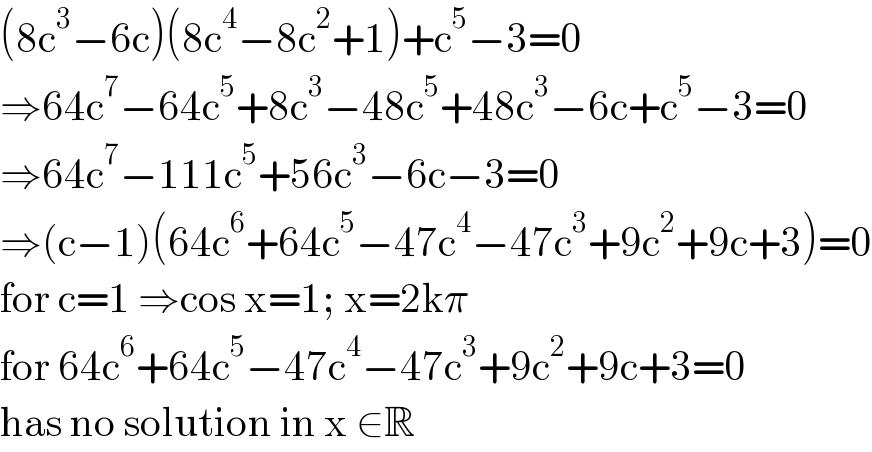
(8c^3 −6c)(8c^4 −8c^2 +1)+c^5 −3=0 ⇒64c^7 −64c^5 +8c^3 −48c^5 +48c^3 −6c+c^5 −3=0 ⇒64c^7 −111c^5 +56c^3 −6c−3=0 ⇒(c−1)(64c^6 +64c^5 −47c^4 −47c^3 +9c^2 +9c+3)=0 for c=1 ⇒cos x=1; x=2kπ for 64c^6 +64c^5 −47c^4 −47c^3 +9c^2 +9c+3=0 has no solution in x ∈R
$$\left(\mathrm{8c}^{\mathrm{3}} −\mathrm{6c}\right)\left(\mathrm{8c}^{\mathrm{4}} −\mathrm{8c}^{\mathrm{2}} +\mathrm{1}\right)+\mathrm{c}^{\mathrm{5}} −\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{64c}^{\mathrm{7}} −\mathrm{64c}^{\mathrm{5}} +\mathrm{8c}^{\mathrm{3}} −\mathrm{48c}^{\mathrm{5}} +\mathrm{48c}^{\mathrm{3}} −\mathrm{6c}+\mathrm{c}^{\mathrm{5}} −\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{64c}^{\mathrm{7}} −\mathrm{111c}^{\mathrm{5}} +\mathrm{56c}^{\mathrm{3}} −\mathrm{6c}−\mathrm{3}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{c}−\mathrm{1}\right)\left(\mathrm{64c}^{\mathrm{6}} +\mathrm{64c}^{\mathrm{5}} −\mathrm{47c}^{\mathrm{4}} −\mathrm{47c}^{\mathrm{3}} +\mathrm{9c}^{\mathrm{2}} +\mathrm{9c}+\mathrm{3}\right)=\mathrm{0} \\ $$$$\mathrm{for}\:\mathrm{c}=\mathrm{1}\:\Rightarrow\mathrm{cos}\:\mathrm{x}=\mathrm{1};\:\mathrm{x}=\mathrm{2k}\pi \\ $$$$\mathrm{for}\:\mathrm{64c}^{\mathrm{6}} +\mathrm{64c}^{\mathrm{5}} −\mathrm{47c}^{\mathrm{4}} −\mathrm{47c}^{\mathrm{3}} +\mathrm{9c}^{\mathrm{2}} +\mathrm{9c}+\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{has}\:\mathrm{no}\:\mathrm{solution}\:\mathrm{in}\:\mathrm{x}\:\in\mathbb{R} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *