Find-all-the-roots-of-z-4-16i-0-

Question Number 54991 by Tawa1 last updated on 15/Feb/19

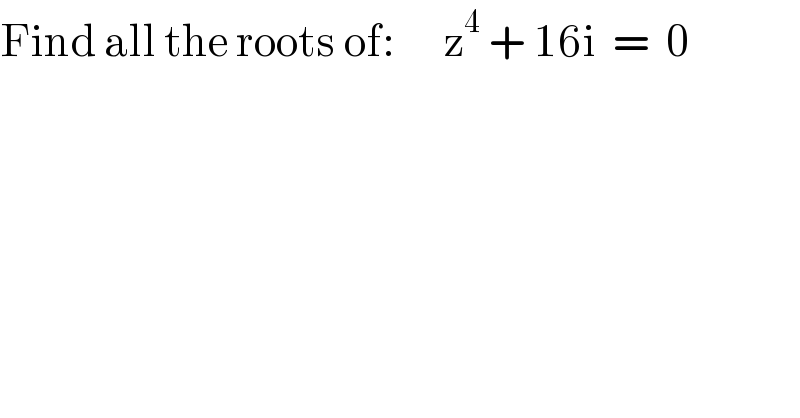
Find all the roots of : z^{4} + 16 i = 0

Commented by maxmathsup by imad last updated on 15/Feb/19

z^{4} + 16 i = 0 \Leftrightarrow z^{4} = - 16 i l e t z = r e^{i θ} \Rightarrow r^{4} e^{i 4 θ} = 16 (- i) = 16 e^{- \frac{i π}{2}} \Rightarrow

r^{4} = 16 a n d 4 θ = - \frac{π}{2} + 2 k π \Rightarrow r = 2 a n d θ_{k} = - \frac{π}{8} + \frac{k π}{2} a n d k \in [[0, 3]] s o t h e r o o t s

o f t h i s e q u a t i o n a r e z_{k} = 2 e^{i (- \frac{π}{8} + \frac{k π}{2})} \Rightarrow z_{0} = 2 e^{- \frac{i π}{8}}

z_{1} = 2 e^{i (\frac{3 π}{8})}, z_{2} = 2 e^{i (\frac{7 π}{8})}, z_{3} = 2 e^{i (\frac{11 π}{8})} a l s o w e h a v e

z^{4} + 16 i = (z - z_{0}) (z - z_{1}) (z - z_{2}) (z - z_{3}) .

Commented by Tawa1 last updated on 16/Feb/19

God bless you sir .

Commented by maxmathsup by imad last updated on 16/Feb/19

y o u a r e w e l c o m e s i r .