Find-an-equation-of-the-tangen-line-to-the-graph-of-the-given-equation-at-the-indicated-point-P-1-xy-16-0-P-2-8-2-y-2-4x-2-5-P-1-3-3-2x-3-x-2-y-y-3-1-0-P-2-3-4-3y-4-4x-x-2-sin

Question Number 156106 by zainaltanjung last updated on 08/Oct/21

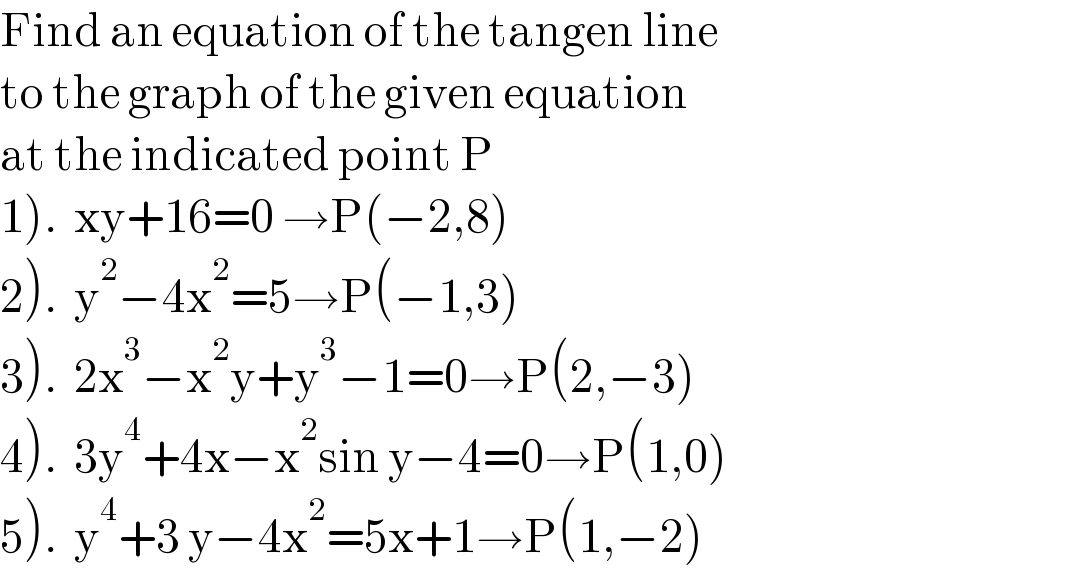
$$\mathrm{Find}\:\mathrm{an}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{tangen}\:\mathrm{line} \\ $$$$\mathrm{to}\:\mathrm{the}\:\mathrm{graph}\:\mathrm{of}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation}\: \\ $$$$\mathrm{at}\:\mathrm{the}\:\mathrm{indicated}\:\mathrm{point}\:\mathrm{P} \\ $$$$\left.\mathrm{1}\right).\:\:\mathrm{xy}+\mathrm{16}=\mathrm{0}\:\rightarrow\mathrm{P}\left(−\mathrm{2},\mathrm{8}\right) \\ $$$$\left.\mathrm{2}\right).\:\:\mathrm{y}^{\mathrm{2}} −\mathrm{4x}^{\mathrm{2}} =\mathrm{5}\rightarrow\mathrm{P}\left(−\mathrm{1},\mathrm{3}\right) \\ $$$$\left.\mathrm{3}\right).\:\:\mathrm{2x}^{\mathrm{3}} −\mathrm{x}^{\mathrm{2}} \mathrm{y}+\mathrm{y}^{\mathrm{3}} −\mathrm{1}=\mathrm{0}\rightarrow\mathrm{P}\left(\mathrm{2},−\mathrm{3}\right) \\ $$$$\left.\mathrm{4}\right).\:\:\mathrm{3y}^{\mathrm{4}} +\mathrm{4x}−\mathrm{x}^{\mathrm{2}} \mathrm{sin}\:\mathrm{y}−\mathrm{4}=\mathrm{0}\rightarrow\mathrm{P}\left(\mathrm{1},\mathrm{0}\right) \\ $$$$\left.\mathrm{5}\right).\:\:\mathrm{y}^{\mathrm{4}} +\mathrm{3}\:\mathrm{y}−\mathrm{4x}^{\mathrm{2}} =\mathrm{5x}+\mathrm{1}\rightarrow\mathrm{P}\left(\mathrm{1},−\mathrm{2}\right) \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com