Menu Close

find-arctan-1-u-1-u-du-

Tinku Tara 0 Comments
Pin




Question Number 86957 by abdomathmax last updated on 01/Apr/20
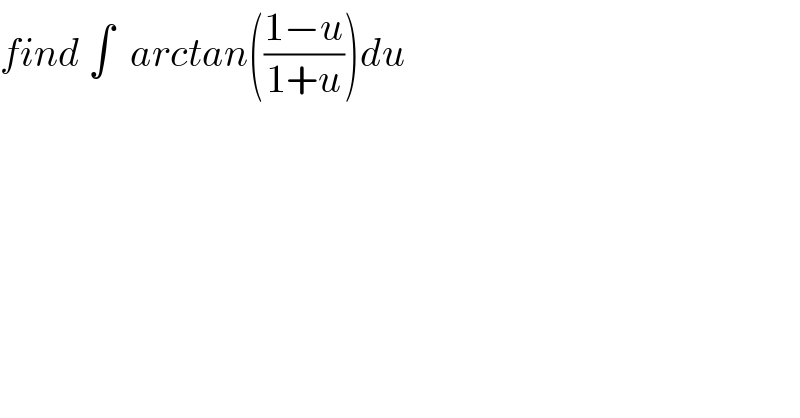
find ∫ arctan(((1−u)/(1+u)))du
$${find}\:\int\:\:{arctan}\left(\frac{\mathrm{1}−{u}}{\mathrm{1}+{u}}\right){du} \\ $$
Commented by Ar Brandon last updated on 01/Apr/20
I=∫arctan(((1−x)/(1+x)))dx Let u=arctan(((1−x)/(1+x))) ⇔ u=arctan(t) with t=((1−x)/(1+x)) ⇒(du/dx)=(du/dt)×(dt/du) (du/dt)=(1/(1+t^2 )) (dt/du)=((−(1+x)−(1−x))/((1+x)^2 ))=((−2)/((1+x)^2 )) ⇒(du/dx)=(1/(1+(((1−x)/(1+x)))^2 ))×((−2)/((1+x)^2 ))=(((1+x)^2 )/((1+x)^2 +(1−x)^2 ))×((−2)/((1+x)^2 ))=((−2)/((1+2x+x^2 )+(1−2x+x^2 ))) ⇒(du/dx)=−(1/(1+x^2 ))⇒du=−(1/(1+x^2 ))dx Let also dv=dx⇒v=x Thus I=x arctan(((1−x)/(1+x)))+∫(x/(1+x^2 ))dx =x arctan(((1−x)/(1+x )))+(1/2)ln(1+x^2 )+C ∫arctan(((1−u)/(1+u)))du=u arctan(((1−u)/(1+u)))+(1/2)ln(1+u^2 )+C C∈R
$${I}=\int{arctan}\left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right){dx} \\ $$$${Let}\:{u}={arctan}\left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)\:\Leftrightarrow\:{u}={arctan}\left({t}\right)\:\:{with}\:\:{t}=\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}} \\ $$$$\Rightarrow\frac{{du}}{{dx}}=\frac{{du}}{{dt}}×\frac{{dt}}{{du}} \\ $$$$\frac{{du}}{{dt}}=\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\:\frac{{dt}}{{du}}=\frac{−\left(\mathrm{1}+{x}\right)−\left(\mathrm{1}−{x}\right)}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }=\frac{−\mathrm{2}}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{du}}{{dx}}=\frac{\mathrm{1}}{\mathrm{1}+\left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)^{\mathrm{2}} }×\frac{−\mathrm{2}}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }=\frac{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} +\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }×\frac{−\mathrm{2}}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }=\frac{−\mathrm{2}}{\left(\mathrm{1}+\mathrm{2}{x}+{x}^{\mathrm{2}} \right)+\left(\mathrm{1}−\mathrm{2}{x}+{x}^{\mathrm{2}} \right)} \\ $$$$\Rightarrow\frac{{du}}{{dx}}=−\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\Rightarrow{du}=−\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$ \\ $$$${Let}\:{also}\:\:\:{dv}={dx}\Rightarrow{v}={x} \\ $$$$ \\ $$$${Thus}\:\:{I}={x}\:{arctan}\left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)+\int\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={x}\:{arctan}\left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}\:}\right)+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)+{C} \\ $$$$\int{arctan}\left(\frac{\mathrm{1}−{u}}{\mathrm{1}+{u}}\right){du}={u}\:{arctan}\left(\frac{\mathrm{1}−{u}}{\mathrm{1}+{u}}\right)+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)+{C} \\ $$$${C}\in\mathbb{R} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\: \\ $$
Commented by mathmax by abdo last updated on 01/Apr/20
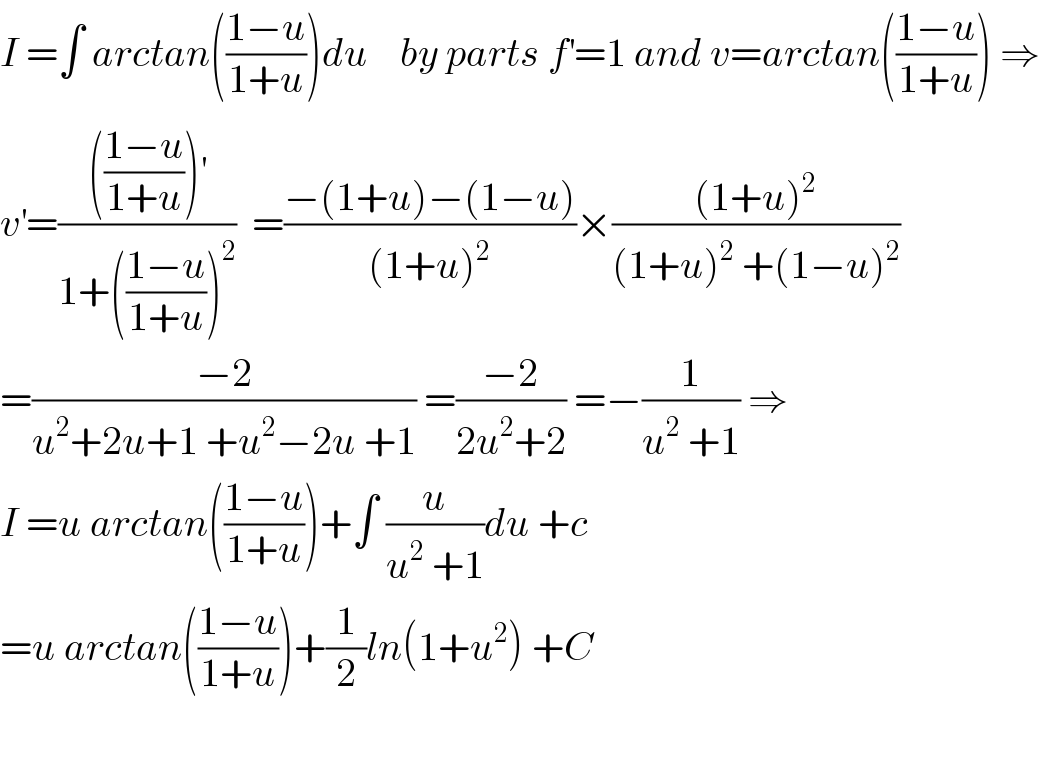
I =∫ arctan(((1−u)/(1+u)))du by parts f^′ =1 and v=arctan(((1−u)/(1+u))) ⇒ v^′ =(((((1−u)/(1+u)))^′ )/(1+(((1−u)/(1+u)))^2 )) =((−(1+u)−(1−u))/((1+u)^2 ))×(((1+u)^2 )/((1+u)^2 +(1−u)^2 )) =((−2)/(u^2 +2u+1 +u^2 −2u +1)) =((−2)/(2u^2 +2)) =−(1/(u^2 +1)) ⇒ I =u arctan(((1−u)/(1+u)))+∫ (u/(u^2 +1))du +c =u arctan(((1−u)/(1+u)))+(1/2)ln(1+u^2 ) +C
$${I}\:=\int\:{arctan}\left(\frac{\mathrm{1}−{u}}{\mathrm{1}+{u}}\right){du}\:\:\:\:{by}\:{parts}\:{f}^{'} =\mathrm{1}\:{and}\:{v}={arctan}\left(\frac{\mathrm{1}−{u}}{\mathrm{1}+{u}}\right)\:\Rightarrow \\ $$$${v}^{'} =\frac{\left(\frac{\mathrm{1}−{u}}{\mathrm{1}+{u}}\right)^{'} }{\mathrm{1}+\left(\frac{\mathrm{1}−{u}}{\mathrm{1}+{u}}\right)^{\mathrm{2}} }\:\:=\frac{−\left(\mathrm{1}+{u}\right)−\left(\mathrm{1}−{u}\right)}{\left(\mathrm{1}+{u}\right)^{\mathrm{2}} }×\frac{\left(\mathrm{1}+{u}\right)^{\mathrm{2}} }{\left(\mathrm{1}+{u}\right)^{\mathrm{2}} \:+\left(\mathrm{1}−{u}\right)^{\mathrm{2}} } \\ $$$$=\frac{−\mathrm{2}}{{u}^{\mathrm{2}} +\mathrm{2}{u}+\mathrm{1}\:+{u}^{\mathrm{2}} −\mathrm{2}{u}\:+\mathrm{1}}\:=\frac{−\mathrm{2}}{\mathrm{2}{u}^{\mathrm{2}} +\mathrm{2}}\:=−\frac{\mathrm{1}}{{u}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$${I}\:={u}\:{arctan}\left(\frac{\mathrm{1}−{u}}{\mathrm{1}+{u}}\right)+\int\:\frac{{u}}{{u}^{\mathrm{2}} \:+\mathrm{1}}{du}\:+{c} \\ $$$$={u}\:{arctan}\left(\frac{\mathrm{1}−{u}}{\mathrm{1}+{u}}\right)+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\:+{C}\:\: \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *