Question Number 96959 by mathmax by abdo last updated on 05/Jun/20
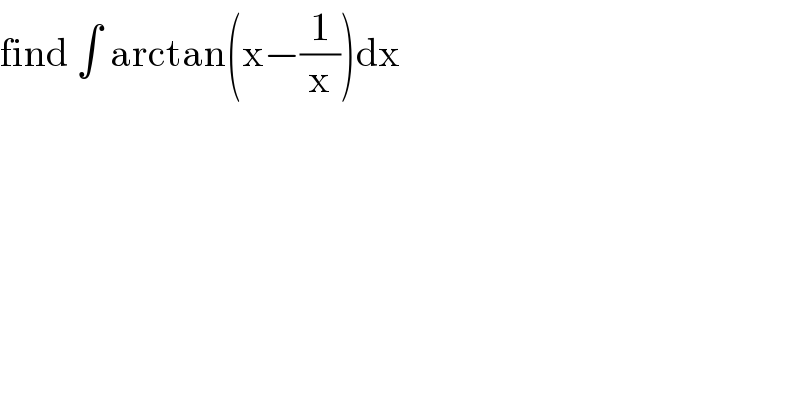
$$\mathrm{find}\:\int\:\mathrm{arctan}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)\mathrm{dx} \\ $$
Answered by MJS last updated on 06/Jun/20

$$\mathrm{by}\:\mathrm{parts} \\ $$$${u}=\mathrm{arctan}\:\left({x}−\frac{\mathrm{1}}{{x}}\right)\:\rightarrow\:{u}'=\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$${v}'=\mathrm{1}\:\rightarrow\:{v}={x} \\ $$$$\int\mathrm{arctan}\:\left({x}−\frac{\mathrm{1}}{{x}}\right)\:{dx}= \\ $$$$={x}\mathrm{arctan}\:\left({x}−\frac{\mathrm{1}}{{x}}\right)\:−\int\frac{{x}^{\mathrm{3}} +{x}}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$\int\frac{{x}^{\mathrm{3}} +{x}}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}}{dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{x}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}}{dx}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{x}}{{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}}{dx}= \\ $$$$… \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right)\:+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left(\mathrm{arctan}\:\left(\mathrm{2}{x}−\sqrt{\mathrm{3}}\right)\:−\mathrm{arctan}\:\left(\mathrm{2}{x}+\sqrt{\mathrm{3}}\right)\right. \\ $$$$\mathrm{now}\:\mathrm{put}\:\mathrm{the}\:\mathrm{parts}\:\mathrm{together} \\ $$
Commented by abdomathmax last updated on 06/Jun/20

$$\mathrm{thanks}\:\mathrm{sir}. \\ $$
