find-arctan-x-arctany-at-form-of-arctan-

Question Number 98187 by abdomathmax last updated on 12/Jun/20

$$\mathrm{find}\:\mathrm{arctan}\left(\mathrm{x}\right)+\mathrm{arctany}\:\:\mathrm{at}\:\mathrm{form}\:\mathrm{of}\:\mathrm{arctan} \\ $$

Answered by Rio Michael last updated on 12/Jun/20

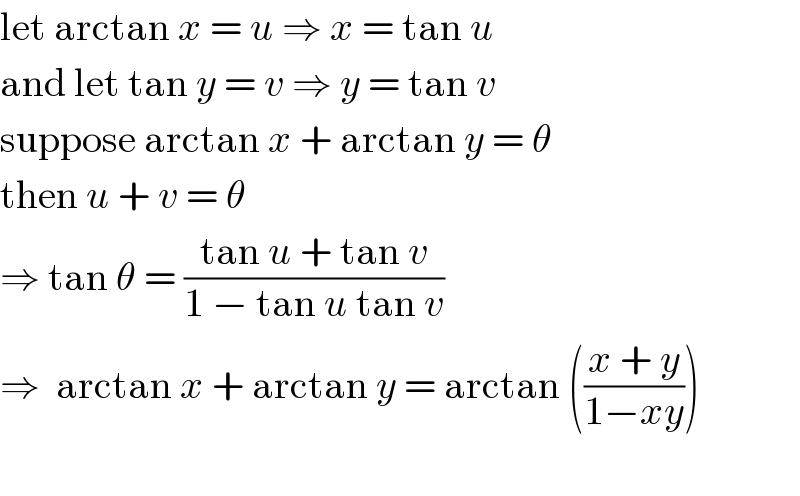
let arctan x = u ⇒ x = tan u and let tan y = v ⇒ y = tan v suppose arctan x + arctan y = θ then u + v = θ ⇒ tan θ = ((tan u + tan v)/(1 − tan u tan v)) ⇒ arctan x + arctan y = arctan (((x + y)/(1−xy)))

$$\mathrm{let}\:\mathrm{arctan}\:{x}\:=\:{u}\:\Rightarrow\:{x}\:=\:\mathrm{tan}\:{u} \\ $$$$\mathrm{and}\:\mathrm{let}\:\mathrm{tan}\:{y}\:=\:{v}\:\Rightarrow\:{y}\:=\:\mathrm{tan}\:{v} \\ $$$$\mathrm{suppose}\:\mathrm{arctan}\:{x}\:+\:\mathrm{arctan}\:{y}\:=\:\theta \\ $$$$\mathrm{then}\:{u}\:+\:{v}\:=\:\theta \\ $$$$\Rightarrow\:\mathrm{tan}\:\theta\:=\:\frac{\mathrm{tan}\:{u}\:+\:\mathrm{tan}\:{v}}{\mathrm{1}\:−\:\mathrm{tan}\:{u}\:\mathrm{tan}\:{v}} \\ $$$$\Rightarrow\:\:\mathrm{arctan}\:{x}\:+\:\mathrm{arctan}\:{y}\:=\:\mathrm{arctan}\:\left(\frac{{x}\:+\:{y}}{\mathrm{1}−{xy}}\right) \\ $$$$ \\ $$

Answered by 1549442205 last updated on 12/Jun/20

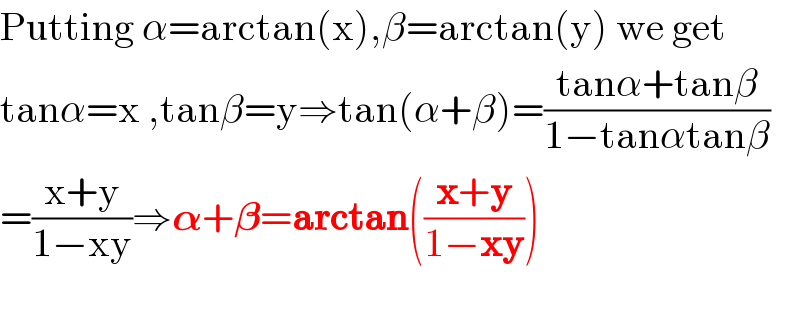
Putting α=arctan(x),β=arctan(y) we get tanα=x ,tanβ=y⇒tan(α+β)=((tanα+tanβ)/(1−tanαtanβ)) =((x+y)/(1−xy))⇒𝛂+𝛃=arctan(((x+y)/(1−xy)))

$$\mathrm{Putting}\:\alpha=\mathrm{arctan}\left(\mathrm{x}\right),\beta=\mathrm{arctan}\left(\mathrm{y}\right)\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{tan}\alpha=\mathrm{x}\:,\mathrm{tan}\beta=\mathrm{y}\Rightarrow\mathrm{tan}\left(\alpha+\beta\right)=\frac{\mathrm{tan}\alpha+\mathrm{tan}\beta}{\mathrm{1}−\mathrm{tan}\alpha\mathrm{tan}\beta} \\ $$$$=\frac{\mathrm{x}+\mathrm{y}}{\mathrm{1}−\mathrm{xy}}\Rightarrow\boldsymbol{\alpha}+\boldsymbol{\beta}=\boldsymbol{\mathrm{arctan}}\left(\frac{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}}{\mathrm{1}−\boldsymbol{\mathrm{xy}}}\right) \\ $$$$ \\ $$

Answered by mathmax by abdo last updated on 12/Jun/20

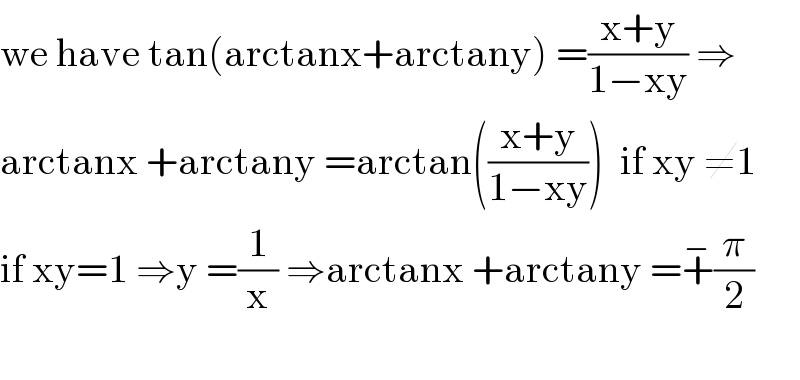
we have tan(arctanx+arctany) =((x+y)/(1−xy)) ⇒ arctanx +arctany =arctan(((x+y)/(1−xy))) if xy ≠1 if xy=1 ⇒y =(1/x) ⇒arctanx +arctany =+^− (π/2)

$$\mathrm{we}\:\mathrm{have}\:\mathrm{tan}\left(\mathrm{arctanx}+\mathrm{arctany}\right)\:=\frac{\mathrm{x}+\mathrm{y}}{\mathrm{1}−\mathrm{xy}}\:\Rightarrow \\ $$$$\mathrm{arctanx}\:+\mathrm{arctany}\:=\mathrm{arctan}\left(\frac{\mathrm{x}+\mathrm{y}}{\mathrm{1}−\mathrm{xy}}\right)\:\:\mathrm{if}\:\mathrm{xy}\:\neq\mathrm{1} \\ $$$$\mathrm{if}\:\mathrm{xy}=\mathrm{1}\:\Rightarrow\mathrm{y}\:=\frac{\mathrm{1}}{\mathrm{x}}\:\Rightarrow\mathrm{arctanx}\:+\mathrm{arctany}\:=\overset{−} {+}\frac{\pi}{\mathrm{2}} \\ $$$$ \\ $$

Facebook Tweet Pin

find-arctan-x-arctany-at-form-of-arctan-

Leave a Reply Cancel reply