Menu Close

find-arctan-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 47540 by maxmathsup by imad last updated on 11/Nov/18
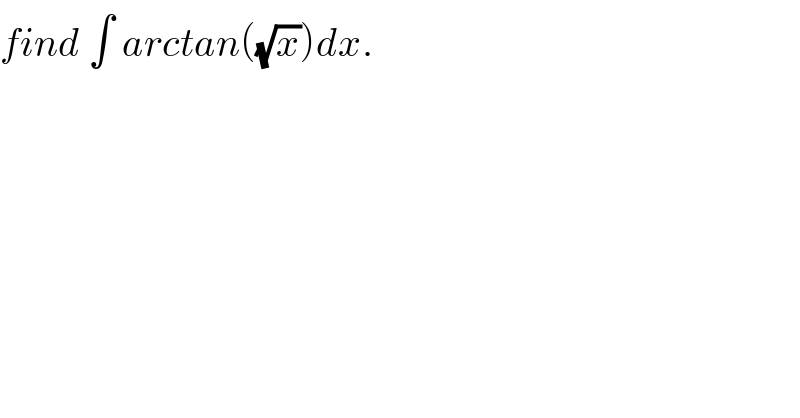
find ∫ arctan((√x))dx.
$${find}\:\int\:{arctan}\left(\sqrt{{x}}\right){dx}. \\ $$
Commented by maxmathsup by imad last updated on 16/Nov/18
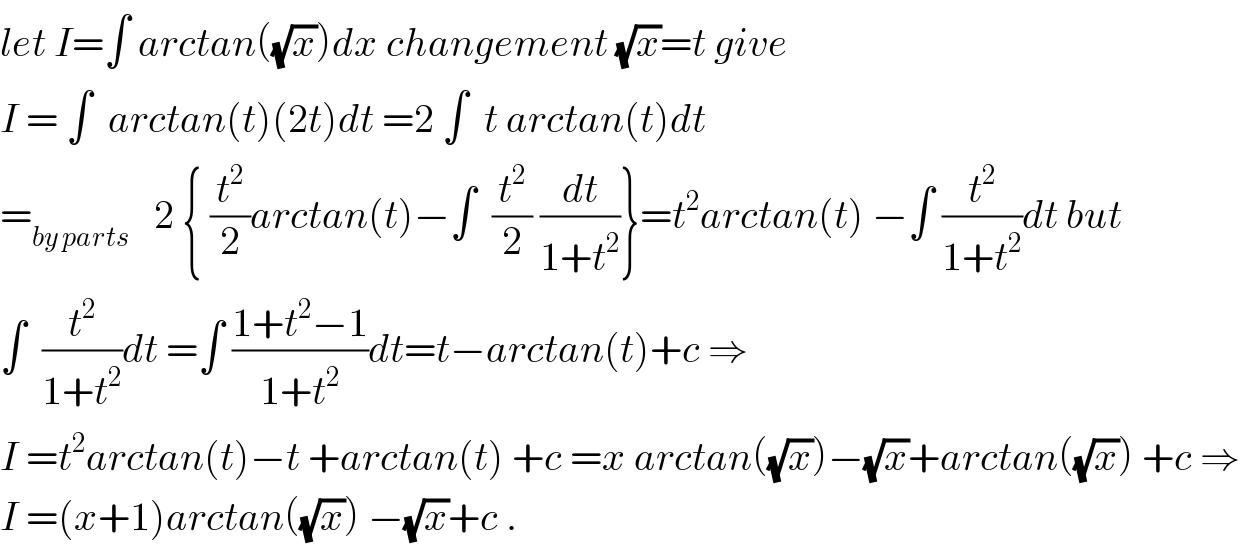
let I=∫ arctan((√x))dx changement (√x)=t give I = ∫ arctan(t)(2t)dt =2 ∫ t arctan(t)dt =_(by parts) 2 { (t^2 /2)arctan(t)−∫ (t^2 /2) (dt/(1+t^2 ))}=t^2 arctan(t) −∫ (t^2 /(1+t^2 ))dt but ∫ (t^2 /(1+t^2 ))dt =∫ ((1+t^2 −1)/(1+t^2 ))dt=t−arctan(t)+c ⇒ I =t^2 arctan(t)−t +arctan(t) +c =x arctan((√x))−(√x)+arctan((√x)) +c ⇒ I =(x+1)arctan((√x)) −(√x)+c .
$${let}\:{I}=\int\:{arctan}\left(\sqrt{{x}}\right){dx}\:{changement}\:\sqrt{{x}}={t}\:{give} \\ $$$${I}\:=\:\int\:\:{arctan}\left({t}\right)\left(\mathrm{2}{t}\right){dt}\:=\mathrm{2}\:\int\:\:{t}\:{arctan}\left({t}\right){dt} \\ $$$$=_{{by}\:{parts}} \:\:\:\mathrm{2}\:\left\{\:\frac{{t}^{\mathrm{2}} }{\mathrm{2}}{arctan}\left({t}\right)−\int\:\:\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\right\}={t}^{\mathrm{2}} {arctan}\left({t}\right)\:−\int\:\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:{but} \\ $$$$\int\:\:\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:=\int\:\frac{\mathrm{1}+{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}={t}−{arctan}\left({t}\right)+{c}\:\Rightarrow \\ $$$${I}\:={t}^{\mathrm{2}} {arctan}\left({t}\right)−{t}\:+{arctan}\left({t}\right)\:+{c}\:={x}\:{arctan}\left(\sqrt{{x}}\right)−\sqrt{{x}}+{arctan}\left(\sqrt{{x}}\right)\:+{c}\:\Rightarrow \\ $$$${I}\:=\left({x}+\mathrm{1}\right){arctan}\left(\sqrt{{x}}\right)\:−\sqrt{{x}}+{c}\:. \\ $$
Answered by arcana last updated on 11/Nov/18
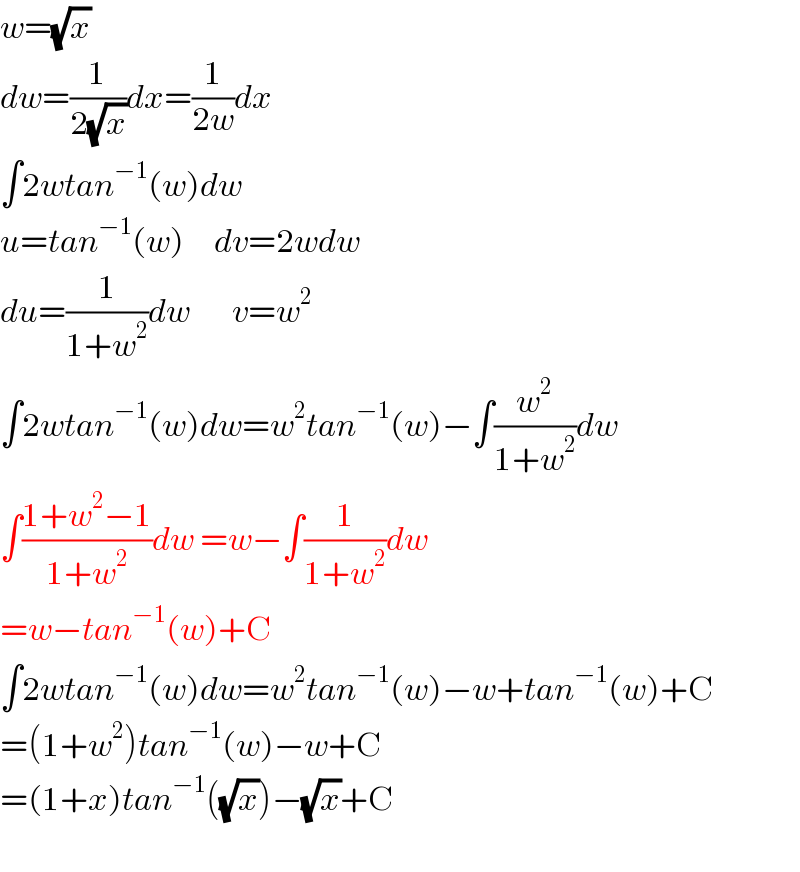
w=(√x) dw=(1/(2(√x)))dx=(1/(2w))dx ∫2wtan^(−1) (w)dw u=tan^(−1) (w) dv=2wdw du=(1/(1+w^2 ))dw v=w^2 ∫2wtan^(−1) (w)dw=w^2 tan^(−1) (w)−∫(w^2 /(1+w^2 ))dw ∫((1+w^2 −1)/(1+w^2 ))dw =w−∫(1/(1+w^2 ))dw =w−tan^(−1) (w)+C ∫2wtan^(−1) (w)dw=w^2 tan^(−1) (w)−w+tan^(−1) (w)+C =(1+w^2 )tan^(−1) (w)−w+C =(1+x)tan^(−1) ((√x))−(√x)+C
$${w}=\sqrt{{x}} \\ $$$${dw}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}{dx}=\frac{\mathrm{1}}{\mathrm{2}{w}}{dx} \\ $$$$\int\mathrm{2}{wtan}^{−\mathrm{1}} \left({w}\right){dw} \\ $$$${u}={tan}^{−\mathrm{1}} \left({w}\right)\:\:\:\:\:{dv}=\mathrm{2}{wdw} \\ $$$${du}=\frac{\mathrm{1}}{\mathrm{1}+{w}^{\mathrm{2}} }{dw}\:\:\:\:\:\:\:{v}={w}^{\mathrm{2}} \\ $$$$\int\mathrm{2}{wtan}^{−\mathrm{1}} \left({w}\right){dw}={w}^{\mathrm{2}} {tan}^{−\mathrm{1}} \left({w}\right)−\int\frac{{w}^{\mathrm{2}} }{\mathrm{1}+{w}^{\mathrm{2}} }{dw} \\ $$$$\int\frac{\mathrm{1}+{w}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}+{w}^{\mathrm{2}} }{dw}\:={w}−\int\frac{\mathrm{1}}{\mathrm{1}+{w}^{\mathrm{2}} }{dw} \\ $$$$={w}−{tan}^{−\mathrm{1}} \left({w}\right)+\mathrm{C} \\ $$$$\int\mathrm{2}{wtan}^{−\mathrm{1}} \left({w}\right){dw}={w}^{\mathrm{2}} {tan}^{−\mathrm{1}} \left({w}\right)−{w}+{tan}^{−\mathrm{1}} \left({w}\right)+\mathrm{C} \\ $$$$=\left(\mathrm{1}+{w}^{\mathrm{2}} \right){tan}^{−\mathrm{1}} \left({w}\right)−{w}+\mathrm{C} \\ $$$$=\left(\mathrm{1}+{x}\right){tan}^{−\mathrm{1}} \left(\sqrt{{x}}\right)−\sqrt{{x}}+\mathrm{C} \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 16/Nov/18
correct answer thanks Arcana.
$${correct}\:{answer}\:{thanks}\:{Arcana}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *