Question Number 18961 by Tinkutara last updated on 02/Aug/17
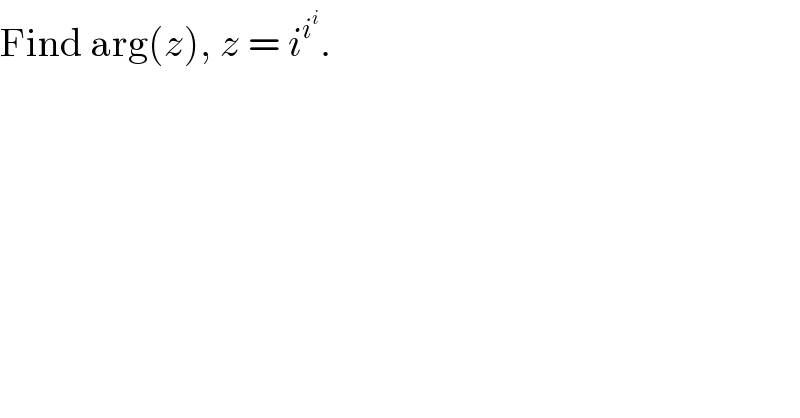
$$\mathrm{Find}\:\mathrm{arg}\left({z}\right),\:{z}\:=\:{i}^{{i}^{{i}} } . \\ $$
Answered by sma3l2996 last updated on 02/Aug/17
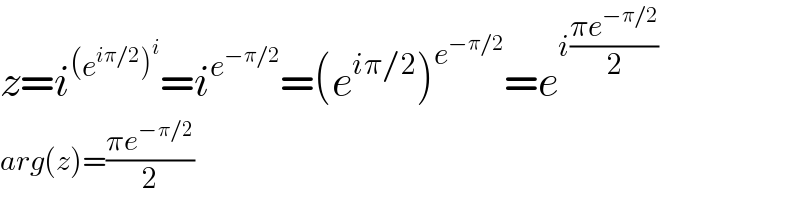
$${z}={i}^{\left({e}^{{i}\pi/\mathrm{2}} \right)^{{i}} } ={i}^{{e}^{−\pi/\mathrm{2}} } =\left({e}^{{i}\pi/\mathrm{2}} \right)^{{e}^{−\pi/\mathrm{2}} } ={e}^{{i}\frac{\pi{e}^{−\pi/\mathrm{2}} }{\mathrm{2}}} \\ $$$${arg}\left({z}\right)=\frac{\pi{e}^{−\pi/\mathrm{2}} }{\mathrm{2}} \\ $$
Commented by Tinkutara last updated on 02/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
