Question Number 34286 by math khazana by abdo last updated on 03/May/18
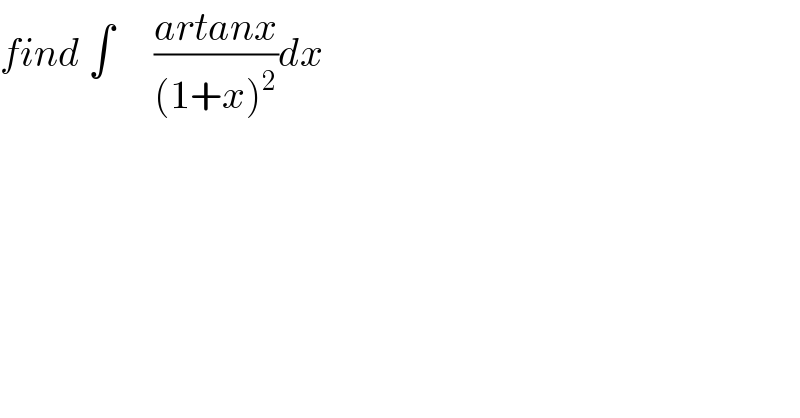
$${find}\:\int\:\:\:\:\:\frac{{artanx}}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }{dx}\: \\ $$
Commented by math khazana by abdo last updated on 07/May/18

$${let}\:{put}\:{I}\:\:=\int\:\:\:\:\frac{{arctanx}}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }\:{dx}\:\:{changement} \\ $$$${x}\:={tan}\theta\:\:{give} \\ $$$${I}\:\:=\:\int\:\:\:\:\:\frac{\theta}{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} }\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta\:=\:\int\:\:\:\frac{\theta{d}\theta}{\mathrm{1}+{tan}^{\mathrm{2}} \theta} \\ $$$$=\int\:\theta\:{cos}^{\mathrm{2}} \theta\:{d}\theta\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\theta\left(\:\mathrm{1}+{cos}\left(\mathrm{2}\theta\right){d}\theta\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\theta\:{d}\theta\:\:\:+\frac{\mathrm{1}}{\mathrm{4}}{sin}\left(\mathrm{2}\theta\right) \\ $$$${I}=\frac{\theta^{\mathrm{2}} }{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{4}}\:{sin}\left(\mathrm{2}\theta\right)\:=\frac{\mathrm{1}}{\mathrm{4}}\left({arctanx}\right)^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{4}}{sin}\left(\mathrm{2}{arctanx}\right)\:+{c} \\ $$
Commented by math khazana by abdo last updated on 08/May/18
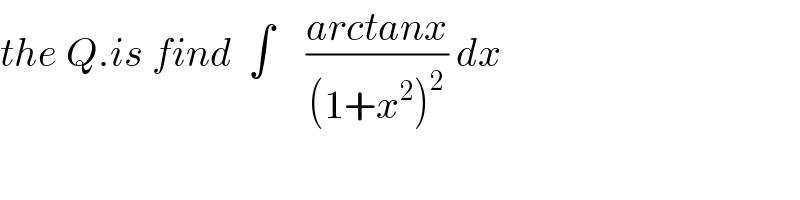
$${the}\:{Q}.{is}\:{find}\:\:\int\:\:\:\:\frac{{arctanx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dx} \\ $$
