Menu Close

find-ch-acosx-bsinx-x-2-x-1-dx-a-and-b-reals-given-

Tinku Tara 0 Comments
Pin




Question Number 90040 by abdomathmax last updated on 21/Apr/20
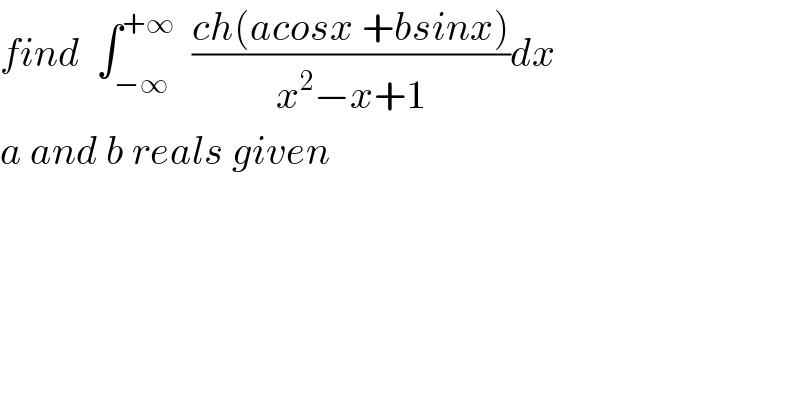
find ∫_(−∞) ^(+∞) ((ch(acosx +bsinx))/(x^2 −x+1))dx a and b reals given
$${find}\:\:\int_{−\infty} ^{+\infty} \:\:\frac{{ch}\left({acosx}\:+{bsinx}\right)}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx} \\ $$$${a}\:{and}\:{b}\:{reals}\:{given} \\ $$
Commented by mathmax by abdo last updated on 22/Apr/20
A =∫_(−∞) ^(+∞) ((ch(acosx +bsinx))/(x^2 −x+1))dx let ϕ(z) =((ch(acosz +bsinz))/(z^2 −z +1)) poles of ϕ? z^2 −z +1 =0 →Δ=−3 ⇒z_1 =((1+i(√3))/2) =e^((iπ)/3) z_2 =((1−i(√3))/2)=e^(−((iπ)/3)) ⇒ϕ(z)=((ch(acosx +bsinx))/((z−e^((iπ)/3) )(z−e^(−((iπ)/3)) ))) residus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(ϕ,e^((iπ)/3) ) =2iπ×((ch(acos(e^((iπ)/3) )+bsin(e^((iπ)/3) )))/(2isin((π/3)))) =π×(2/( (√3)))ch(acos(e^((iπ)/3) )+bsin(e^((iπ)/3) )) cos(e^((iπ)/3) ) =cos((1/2)+i((√3)/2)) =((e^(i((1/2)+i((√3)/2))) +e^(−i((1/2)+((i(√3))/2))) )/2) =(1/2){((e^(−((√3)/2)) ( cos((1/2))+isin((1/2)))+e^((√3)/2) (cos((1/2))−isin((1/2))))/1)} =(1/2){ cos((1/2))(e^((√3)/2) +e^(−((√3)/2)) ) −isin((1/2))(e^((√3)/2) −e^(−((√3)/2)) )} =cos((1/2))ch(((√3)/2))−sin((1/2))sh(((√3)/2))...be continued...
$${A}\:=\int_{−\infty} ^{+\infty} \:\frac{{ch}\left({acosx}\:+{bsinx}\right)}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}\:{let}\:\varphi\left({z}\right)\:=\frac{{ch}\left({acosz}\:+{bsinz}\right)}{{z}^{\mathrm{2}} −{z}\:+\mathrm{1}} \\ $$$${poles}\:{of}\:\varphi?\:\:\:{z}^{\mathrm{2}} −{z}\:+\mathrm{1}\:=\mathrm{0}\:\rightarrow\Delta=−\mathrm{3}\:\Rightarrow{z}_{\mathrm{1}} =\frac{\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:={e}^{\frac{{i}\pi}{\mathrm{3}}} \\ $$$${z}_{\mathrm{2}} =\frac{\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\mathrm{2}}={e}^{−\frac{{i}\pi}{\mathrm{3}}} \:\Rightarrow\varphi\left({z}\right)=\frac{{ch}\left({acosx}\:+{bsinx}\right)}{\left({z}−{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)}\:\:{residus}\:{theorem}\:{give} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\:=\mathrm{2}{i}\pi×\frac{{ch}\left({acos}\left({e}^{\frac{{i}\pi}{\mathrm{3}}} \right)+{bsin}\left({e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\right)}{\mathrm{2}{isin}\left(\frac{\pi}{\mathrm{3}}\right)} \\ $$$$=\pi×\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{ch}\left({acos}\left({e}^{\frac{{i}\pi}{\mathrm{3}}} \right)+{bsin}\left({e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\right) \\ $$$${cos}\left({e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\:={cos}\left(\frac{\mathrm{1}}{\mathrm{2}}+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\:=\frac{{e}^{{i}\left(\frac{\mathrm{1}}{\mathrm{2}}+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)} +{e}^{−{i}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)} }{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{{e}^{−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \left(\:{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+{isin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)+{e}^{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \left({cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−{isin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)}{\mathrm{1}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\left({e}^{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \:+{e}^{−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \right)\:−{isin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\left({e}^{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \:−{e}^{−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \right)\right\} \\ $$$$={cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){ch}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)−{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){sh}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)…{be}\:{continued}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *