Menu Close

Find-constant-a-b-so-that-y-t-t-3-e-2t-is-solution-of-IVP-y-ay-e-2t-y-0-b-

Tinku Tara 0 Comments
Pin




Question Number 182139 by Mastermind last updated on 04/Dec/22
Find constant a, b, so that y(t)=(t+3)e^(2t) is solution of IVP y^′ =ay+e^(2t) , y(0)=b .
$$\mathrm{Find}\:\mathrm{constant}\:\mathrm{a},\:\mathrm{b},\:\mathrm{so}\:\mathrm{that} \\ $$$$\mathrm{y}\left(\mathrm{t}\right)=\left(\mathrm{t}+\mathrm{3}\right)\mathrm{e}^{\mathrm{2t}} \:\mathrm{is}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{IVP} \\ $$$$\mathrm{y}^{'} =\mathrm{ay}+\mathrm{e}^{\mathrm{2t}} ,\:\:\:\:\:\:\:\:\:\:\:\mathrm{y}\left(\mathrm{0}\right)=\mathrm{b} \\ $$$$ \\ $$$$. \\ $$
Commented by mr W last updated on 06/Dec/22
do you never give a feedback when a question of yours is answered?
$${do}\:{you}\:{never}\:{give}\:{a}\:{feedback}\:{when}\:{a} \\ $$$${question}\:{of}\:{yours}\:{is}\:{answered}? \\ $$
Answered by mr W last updated on 04/Dec/22
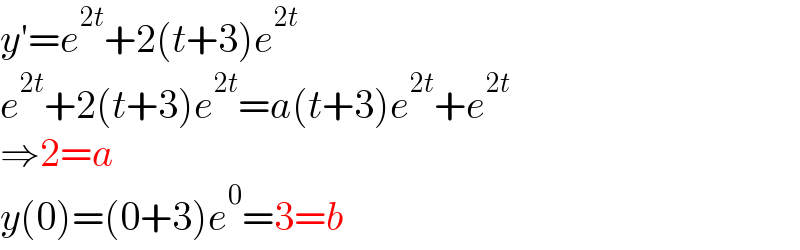
y′=e^(2t) +2(t+3)e^(2t) e^(2t) +2(t+3)e^(2t) =a(t+3)e^(2t) +e^(2t) ⇒2=a y(0)=(0+3)e^0 =3=b
$${y}'={e}^{\mathrm{2}{t}} +\mathrm{2}\left({t}+\mathrm{3}\right){e}^{\mathrm{2}{t}} \\ $$$${e}^{\mathrm{2}{t}} +\mathrm{2}\left({t}+\mathrm{3}\right){e}^{\mathrm{2}{t}} ={a}\left({t}+\mathrm{3}\right){e}^{\mathrm{2}{t}} +{e}^{\mathrm{2}{t}} \\ $$$$\Rightarrow\mathrm{2}={a} \\ $$$${y}\left(\mathrm{0}\right)=\left(\mathrm{0}+\mathrm{3}\right){e}^{\mathrm{0}} =\mathrm{3}={b} \\ $$
Commented by Mastermind last updated on 22/Dec/22
Thank you boss
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{boss} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *