Menu Close

find-cos-2x-2-1-x-4-x-2-3-dx-

Tinku Tara 0 Comments
Pin




Question Number 80452 by abdomathmax last updated on 03/Feb/20
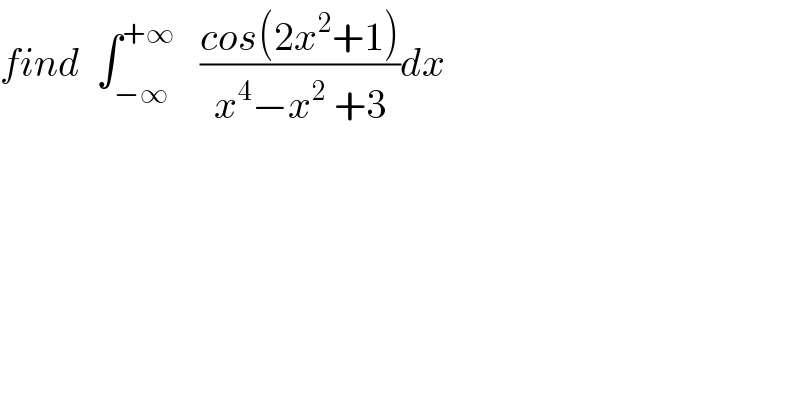
find ∫_(−∞) ^(+∞) ((cos(2x^2 +1))/(x^4 −x^2 +3))dx
$${find}\:\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{cos}\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right)}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} \:+\mathrm{3}}{dx} \\ $$
Commented by abdomathmax last updated on 03/Mar/20
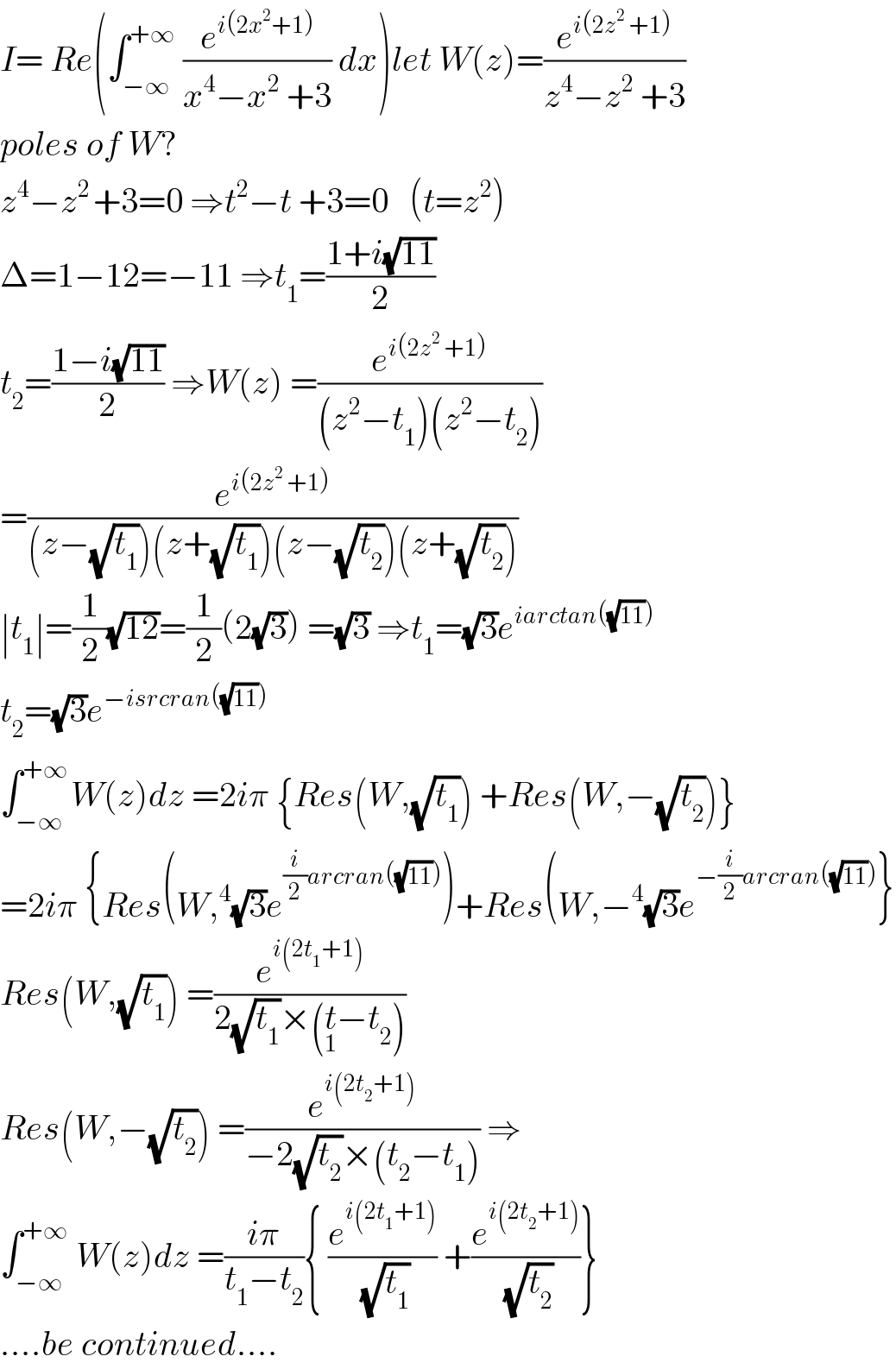
I= Re(∫_(−∞) ^(+∞) (e^(i(2x^2 +1)) /(x^4 −x^2 +3)) dx)let W(z)=(e^(i(2z^2 +1)) /(z^4 −z^2 +3)) poles of W? z^4 −z^(2 ) +3=0 ⇒t^2 −t +3=0 (t=z^2 ) Δ=1−12=−11 ⇒t_1 =((1+i(√(11)))/2) t_2 =((1−i(√(11)))/2) ⇒W(z) =(e^(i(2z^2 +1)) /((z^2 −t_1 )(z^2 −t_2 ))) =(e^(i(2z^2 +1)) /((z−(√t_1 ))(z+(√t_1 ))(z−(√t_2 ))(z+(√t_2 )))) ∣t_1 ∣=(1/2)(√(12))=(1/2)(2(√3)) =(√3) ⇒t_1 =(√3)e^(iarctan((√(11)))) t_2 =(√3)e^(−isrcran((√(11)))) ∫_(−∞) ^(+∞ ) W(z)dz =2iπ {Res(W,(√t_1 )) +Res(W,−(√t_2 ))} =2iπ {Res(W,^4 (√3)e^((i/2)arcran((√(11)))) )+Res(W,−^4 (√3)e^(−(i/2)arcran((√(11)))) } Res(W,(√t_1 )) =(e^(i(2t_1 +1)) /(2(√t_1 )×(t_1 −t_2 ))) Res(W,−(√t_2 )) =(e^(i(2t_2 +1)) /(−2(√t_2 )×(t_2 −t_1 ))) ⇒ ∫_(−∞) ^(+∞) W(z)dz =((iπ)/(t_1 −t_2 )){ (e^(i(2t_1 +1)) /( (√t_1 ))) +(e^(i(2t_2 +1)) /( (√t_2 )))} ....be continued....
$${I}=\:{Re}\left(\int_{−\infty} ^{+\infty} \:\frac{{e}^{{i}\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right)} }{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} \:+\mathrm{3}}\:{dx}\right){let}\:{W}\left({z}\right)=\frac{{e}^{{i}\left(\mathrm{2}{z}^{\mathrm{2}} \:+\mathrm{1}\right)} }{{z}^{\mathrm{4}} −{z}^{\mathrm{2}} \:+\mathrm{3}} \\ $$$${poles}\:{of}\:{W}? \\ $$$${z}^{\mathrm{4}} −{z}^{\mathrm{2}\:} +\mathrm{3}=\mathrm{0}\:\Rightarrow{t}^{\mathrm{2}} −{t}\:+\mathrm{3}=\mathrm{0}\:\:\:\left({t}={z}^{\mathrm{2}} \right) \\ $$$$\Delta=\mathrm{1}−\mathrm{12}=−\mathrm{11}\:\Rightarrow{t}_{\mathrm{1}} =\frac{\mathrm{1}+{i}\sqrt{\mathrm{11}}}{\mathrm{2}} \\ $$$${t}_{\mathrm{2}} =\frac{\mathrm{1}−{i}\sqrt{\mathrm{11}}}{\mathrm{2}}\:\Rightarrow{W}\left({z}\right)\:=\frac{{e}^{{i}\left(\mathrm{2}{z}^{\mathrm{2}} \:+\mathrm{1}\right)} }{\left({z}^{\mathrm{2}} −{t}_{\mathrm{1}} \right)\left({z}^{\mathrm{2}} −{t}_{\mathrm{2}} \right)} \\ $$$$=\frac{{e}^{{i}\left(\mathrm{2}{z}^{\mathrm{2}} \:+\mathrm{1}\right)} }{\left({z}−\sqrt{{t}_{\mathrm{1}} }\right)\left({z}+\sqrt{{t}_{\mathrm{1}} }\right)\left({z}−\sqrt{{t}_{\mathrm{2}} }\right)\left({z}+\sqrt{{t}_{\mathrm{2}} }\right)} \\ $$$$\mid{t}_{\mathrm{1}} \mid=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{12}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}\sqrt{\mathrm{3}}\right)\:=\sqrt{\mathrm{3}}\:\Rightarrow{t}_{\mathrm{1}} =\sqrt{\mathrm{3}}{e}^{{iarctan}\left(\sqrt{\mathrm{11}}\right)} \\ $$$${t}_{\mathrm{2}} =\sqrt{\mathrm{3}}{e}^{−{isrcran}\left(\sqrt{\mathrm{11}}\right)} \\ $$$$\int_{−\infty} ^{+\infty\:} {W}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\left\{{Res}\left({W},\sqrt{{t}_{\mathrm{1}} }\right)\:+{Res}\left({W},−\sqrt{{t}_{\mathrm{2}} }\right)\right\} \\ $$$$=\mathrm{2}{i}\pi\:\left\{{Res}\left({W},^{\mathrm{4}} \sqrt{\mathrm{3}}{e}^{\frac{{i}}{\mathrm{2}}{arcran}\left(\sqrt{\mathrm{11}}\right)} \right)+{Res}\left({W},−^{\mathrm{4}} \sqrt{\mathrm{3}}{e}^{−\frac{{i}}{\mathrm{2}}{arcran}\left(\sqrt{\mathrm{11}}\right)} \right\}\right. \\ $$$${Res}\left({W},\sqrt{{t}_{\mathrm{1}} }\right)\:=\frac{{e}^{{i}\left(\mathrm{2}{t}_{\mathrm{1}} +\mathrm{1}\right)} }{\mathrm{2}\sqrt{{t}_{\mathrm{1}} }×\left(\underset{\mathrm{1}} {{t}}−{t}_{\mathrm{2}} \right)}\: \\ $$$${Res}\left({W},−\sqrt{{t}_{\mathrm{2}} }\right)\:=\frac{{e}^{{i}\left(\mathrm{2}{t}_{\mathrm{2}} +\mathrm{1}\right)} }{−\mathrm{2}\sqrt{{t}_{\mathrm{2}} }×\left({t}_{\mathrm{2}} −{t}_{\mathrm{1}} \right)}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:{W}\left({z}\right){dz}\:=\frac{{i}\pi}{{t}_{\mathrm{1}} −{t}_{\mathrm{2}} }\left\{\:\frac{{e}^{{i}\left(\mathrm{2}{t}_{\mathrm{1}} +\mathrm{1}\right)} }{\:\sqrt{{t}_{\mathrm{1}} }}\:+\frac{{e}^{{i}\left(\mathrm{2}{t}_{\mathrm{2}} +\mathrm{1}\right)} }{\:\sqrt{{t}_{\mathrm{2}} }}\right\} \\ $$$$….{be}\:{continued}…. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *