Question Number 165787 by daus last updated on 08/Feb/22
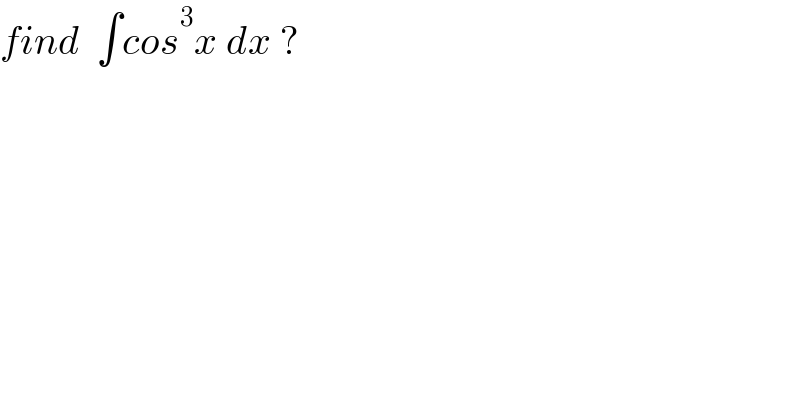
$${find}\:\:\int{cos}^{\mathrm{3}} {x}\:{dx}\:? \\ $$
Answered by aleks041103 last updated on 08/Feb/22
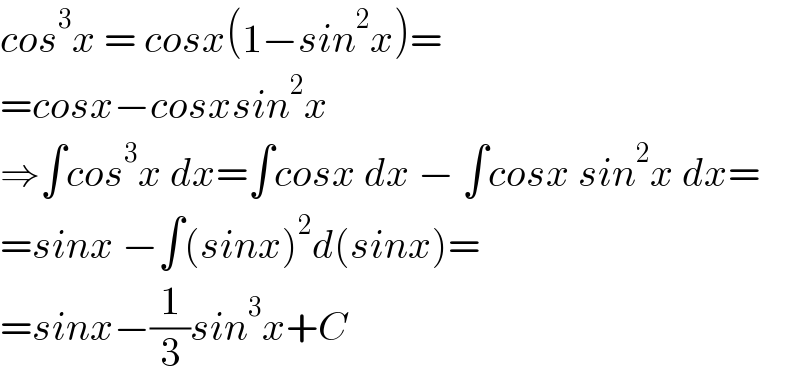
$${cos}^{\mathrm{3}} {x}\:=\:{cosx}\left(\mathrm{1}−{sin}^{\mathrm{2}} {x}\right)= \\ $$$$={cosx}−{cosxsin}^{\mathrm{2}} {x} \\ $$$$\Rightarrow\int{cos}^{\mathrm{3}} {x}\:{dx}=\int{cosx}\:{dx}\:−\:\int{cosx}\:{sin}^{\mathrm{2}} {x}\:{dx}= \\ $$$$={sinx}\:−\int\left({sinx}\right)^{\mathrm{2}} {d}\left({sinx}\right)= \\ $$$$={sinx}−\frac{\mathrm{1}}{\mathrm{3}}{sin}^{\mathrm{3}} {x}+{C} \\ $$
Answered by nurtani last updated on 08/Feb/22
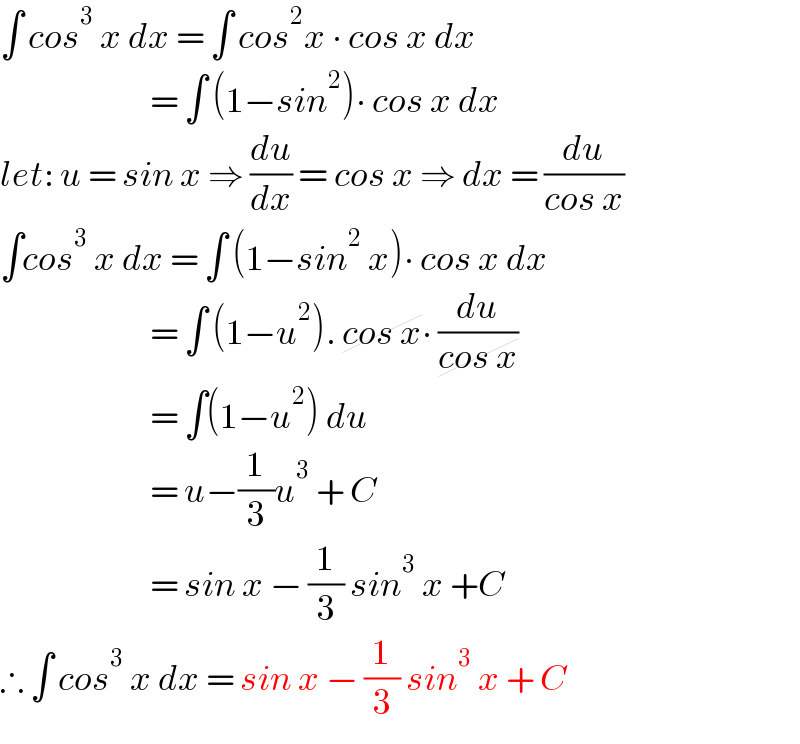
$$\int\:{cos}^{\mathrm{3}} \:{x}\:{dx}\:=\:\int\:{cos}^{\mathrm{2}} {x}\:\centerdot\:{cos}\:{x}\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\int\:\left(\mathrm{1}−{sin}^{\mathrm{2}} \right)\centerdot\:{cos}\:{x}\:{dx} \\ $$$${let}:\:{u}\:=\:{sin}\:{x}\:\Rightarrow\:\frac{{du}}{{dx}}\:=\:{cos}\:{x}\:\Rightarrow\:{dx}\:=\:\frac{{du}}{{cos}\:{x}} \\ $$$$\int{cos}^{\mathrm{3}} \:{x}\:{dx}\:=\:\int\:\left(\mathrm{1}−{sin}^{\mathrm{2}} \:{x}\right)\centerdot\:{cos}\:{x}\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\int\:\left(\mathrm{1}−{u}^{\mathrm{2}} \right).\:\cancel{{cos}\:{x}}\centerdot\:\frac{{du}}{\cancel{{cos}\:{x}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\int\left(\mathrm{1}−{u}^{\mathrm{2}} \right)\:{du} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{u}−\frac{\mathrm{1}}{\mathrm{3}}{u}^{\mathrm{3}} \:+\:{C} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{sin}\:{x}\:−\:\frac{\mathrm{1}}{\mathrm{3}}\:{sin}^{\mathrm{3}} \:{x}\:+{C} \\ $$$$\therefore\:\int\:{cos}^{\mathrm{3}} \:{x}\:{dx}\:=\:{sin}\:{x}\:−\:\frac{\mathrm{1}}{\mathrm{3}}\:{sin}^{\mathrm{3}} \:{x}\:+\:{C} \\ $$
Commented by daus last updated on 08/Feb/22

$${thanks} \\ $$
