Question Number 27598 by abdo imad last updated on 10/Jan/18
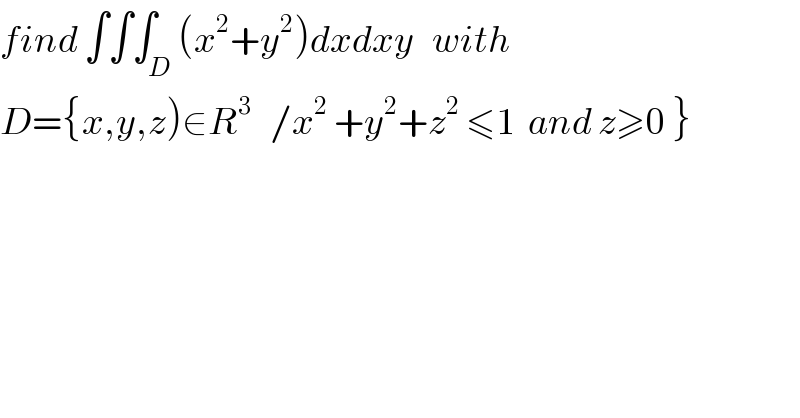
$${find}\:\int\int\int_{{D}} \left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right){dxdxy}\:\:\:{with} \\ $$$$\left.{D}=\left\{{x},{y},{z}\right)\in{R}^{\mathrm{3}} \:\:\:/{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \:\leqslant\mathrm{1}\:\:{and}\:{z}\geqslant\mathrm{0}\:\right\} \\ $$
Commented by abdo imad last updated on 21/Jan/18
![we have z^2 ≤ 1−(x^2 +y^2 ) ≤1 and z≥0 ⇒ 0≤z≤1 so I= ∫∫∫ (x^2 +y^2 +z^2 )dxdydz = ∫_0 ^1 (∫∫_W (x^2 +y^2 )dxdy)dz with W ={ (x,y)∈R^2 / x^2 +y^2 ≤1−z^2 and z≥0} let define a diffeomorphisme on W we use the polar coordinate x=r cosθ and y =rsinθ we must have 0<r ≤(√(1−z^2 )) and 0≤θ≤2π ∫∫_W ( x^2 +y^2 )dxdy= ∫∫_(0<r≤(√(1−z^2 )) and 0≤θ≤2π) r^2 rdrdθ = 2π ∫_0 ^(√(1−z^2 )) r^3 dr = (π/2) [ r^4 ]_0 ^(√(1−z^2 )) = (π/2)(1−z^2 )^2 = (π/2)( z^4 −2z^2 +1) and I= (π/2) ∫_0 ^1 (z^4 −2z^2 +1)dz =(π/2) [ (z^5 /5) −(2/3) z^3 +z]_0 ^1 = (π/2) ( (1/5) −(2/3) +1) = (π/2)( (1/5) +(1/3)) = ((8π)/(30)) = ((4π)/(15)) .](https://www.tinkutara.com/question/Q28136.png)
$${we}\:{have}\:{z}^{\mathrm{2}} \leqslant\:\mathrm{1}−\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\:\leqslant\mathrm{1}\:{and}\:{z}\geqslant\mathrm{0}\:\Rightarrow\:\:\:\mathrm{0}\leqslant{z}\leqslant\mathrm{1}\:{so} \\ $$$${I}=\:\int\int\int\:\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:+{z}^{\mathrm{2}} \right){dxdydz}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\left(\int\int_{{W}} \left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right){dxdy}\right){dz} \\ $$$${with}\:{W}\:=\left\{\:\left({x},{y}\right)\in{R}^{\mathrm{2}} \:/\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:\leqslant\mathrm{1}−{z}^{\mathrm{2}} \:\:{and}\:{z}\geqslant\mathrm{0}\right\}\:{let}\:{define} \\ $$$${a}\:{diffeomorphisme}\:{on}\:{W}\:{we}\:{use}\:{the}\:{polar}\:{coordinate} \\ $$$${x}={r}\:{cos}\theta\:\:{and}\:{y}\:={rsin}\theta\:\:{we}\:{must}\:{have}\:\:\mathrm{0}<{r}\:\leqslant\sqrt{\mathrm{1}−{z}^{\mathrm{2}} } \\ $$$${and}\:\mathrm{0}\leqslant\theta\leqslant\mathrm{2}\pi \\ $$$$\int\int_{{W}} \left(\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right){dxdy}=\:\int\int_{\mathrm{0}<{r}\leqslant\sqrt{\mathrm{1}−{z}^{\mathrm{2}} \:}\:\:{and}\:\mathrm{0}\leqslant\theta\leqslant\mathrm{2}\pi} {r}^{\mathrm{2}} {rdrd}\theta \\ $$$$=\:\mathrm{2}\pi\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{1}−{z}^{\mathrm{2}} }} \:\:\:{r}^{\mathrm{3}} {dr}\:\:=\:\frac{\pi}{\mathrm{2}}\:\left[\:{r}^{\mathrm{4}} \right]_{\mathrm{0}} ^{\sqrt{\mathrm{1}−{z}^{\mathrm{2}} }} \:\:=\:\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−{z}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$=\:\frac{\pi}{\mathrm{2}}\left(\:{z}^{\mathrm{4}} \:−\mathrm{2}{z}^{\mathrm{2}} +\mathrm{1}\right)\:{and} \\ $$$${I}=\:\frac{\pi}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\left({z}^{\mathrm{4}} \:−\mathrm{2}{z}^{\mathrm{2}} +\mathrm{1}\right){dz}\:=\frac{\pi}{\mathrm{2}}\:\left[\:\:\frac{{z}^{\mathrm{5}} }{\mathrm{5}}\:−\frac{\mathrm{2}}{\mathrm{3}}\:{z}^{\mathrm{3}} \:+{z}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\:\frac{\pi}{\mathrm{2}}\:\left(\:\frac{\mathrm{1}}{\mathrm{5}}\:−\frac{\mathrm{2}}{\mathrm{3}}\:+\mathrm{1}\right)\:=\:\frac{\pi}{\mathrm{2}}\left(\:\frac{\mathrm{1}}{\mathrm{5}}\:+\frac{\mathrm{1}}{\mathrm{3}}\right)\:=\:\frac{\mathrm{8}\pi}{\mathrm{30}}\:=\:\frac{\mathrm{4}\pi}{\mathrm{15}}\:. \\ $$$$ \\ $$
