Question Number 28448 by abdo imad last updated on 25/Jan/18

$${find}\:\int\int_{{D}} \:\:\:\:\frac{{xy}}{\mathrm{1}+{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{dxdy}\:{with} \\ $$$${D}=\:\left\{\left({x},{y}\right)\in{R}^{\mathrm{2}} /\:\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \geqslant\mathrm{1}\:\:\right\}\:\:. \\ $$
Answered by ajfour last updated on 26/Jan/18
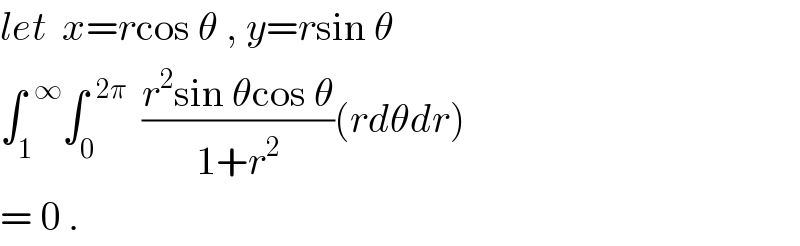
$${let}\:\:{x}={r}\mathrm{cos}\:\theta\:,\:{y}={r}\mathrm{sin}\:\theta \\ $$$$\int_{\mathrm{1}} ^{\:\:\infty} \int_{\mathrm{0}} ^{\:\:\mathrm{2}\pi} \:\:\frac{{r}^{\mathrm{2}} \mathrm{sin}\:\theta\mathrm{cos}\:\theta}{\mathrm{1}+{r}^{\mathrm{2}} }\left({rd}\theta{dr}\right) \\ $$$$=\:\mathrm{0}\:. \\ $$
