Question Number 28160 by abdo imad last updated on 21/Jan/18
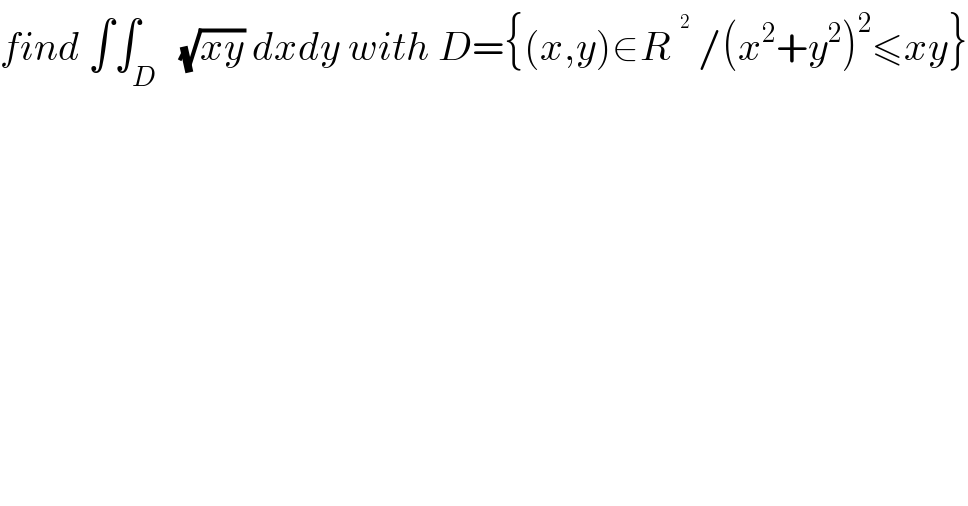
$${find}\:\int\int_{{D}} \:\:\sqrt{{xy}}\:{dxdy}\:{with}\:{D}=\left\{\left({x},{y}\right)\in{R}^{} \:/\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{2}} \leqslant{xy}\right\} \\ $$
Commented by abdo imad last updated on 26/Jan/18
![let put I= ∫∫_D (√(xy)) dxdy let use he ch. x=rcosθ and y= rsinθ ⇒ 0<r^4 < r^2 cosθ sinθ ⇒0 <r^2 < (1/2)sin(2θ) so we must have sin(2θ) >0 ⇒ 0<θ< (π/2) and 0<r< (1/( (√2)))(√(sin(2θ))) I = ∫_0 ^(π/2) ( ∫_0 ^((1/( (√2)))(√(sin(2θ)))) (√(r^2 sinθ cosθ)) rdr)dθ =(1/( (√2)))∫_0 ^(π/2) ( ∫_0 ^((1/( (√2)))(√(sin(2θ)))) r^2 dr)(√(sin(2θ))) dθ =(1/(3(√2))) ∫_0 ^(π/2) [ r^3 ]_0 ^((1/( (√2)))(√(sin(2θ)))) (√(sin(2θ)))dθ =(1/(3(√2))) ∫_0 ^(π/2) ((1/2) sin(2θ)(1/( (√2)))(√(sin(2θ))) )(√(sin(2θ))))dθ = (1/(12)) ∫_0 ^(π/2) sin^2 (2θ)dθ=(1/(12)) ∫_0 ^(π/2) ((1−cos(4θ))/2)dθ](https://www.tinkutara.com/question/Q28452.png)
$${let}\:{put}\:\:{I}=\:\int\int_{{D}} \sqrt{{xy}}\:{dxdy}\:\:\:{let}\:{use}\:{he}\:{ch}.\:{x}={rcos}\theta\:{and} \\ $$$${y}=\:{rsin}\theta\:\:\Rightarrow\:\mathrm{0}<{r}^{\mathrm{4}} <\:{r}^{\mathrm{2}} {cos}\theta\:{sin}\theta\:\Rightarrow\mathrm{0}\:<{r}^{\mathrm{2}} <\:\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}\theta\right) \\ $$$${so}\:{we}\:{must}\:{have}\:{sin}\left(\mathrm{2}\theta\right)\:>\mathrm{0}\:\Rightarrow\:\:\mathrm{0}<\theta<\:\frac{\pi}{\mathrm{2}}\:{and} \\ $$$$\mathrm{0}<{r}<\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\sqrt{{sin}\left(\mathrm{2}\theta\right)}\: \\ $$$${I}\:=\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\sqrt{{sin}\left(\mathrm{2}\theta\right)}} \sqrt{{r}^{\mathrm{2}} {sin}\theta\:{cos}\theta}\:{rdr}\right){d}\theta \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\left(\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\sqrt{{sin}\left(\mathrm{2}\theta\right)}} \:{r}^{\mathrm{2}} {dr}\right)\sqrt{{sin}\left(\mathrm{2}\theta\right)}\:{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{2}}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left[\:{r}^{\mathrm{3}} \right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\sqrt{{sin}\left(\mathrm{2}\theta\right)}} \sqrt{{sin}\left(\mathrm{2}\theta\right)}{d}\theta \\ $$$$\left.\:=\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{2}}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{\mathrm{1}}{\mathrm{2}}\:{sin}\left(\mathrm{2}\theta\right)\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\sqrt{{sin}\left(\mathrm{2}\theta\right)}\:\right)\sqrt{{sin}\left(\mathrm{2}\theta\right)}\right){d}\theta \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{12}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}^{\mathrm{2}} \left(\mathrm{2}\theta\right){d}\theta=\frac{\mathrm{1}}{\mathrm{12}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}−{cos}\left(\mathrm{4}\theta\right)}{\mathrm{2}}{d}\theta \\ $$
Commented by abdo imad last updated on 26/Jan/18
![I= (π/(48)) −(1/(24)) ∫_0 ^(π/2) cos(4θ)dθ= (π/(48)) − (1/(4×24))[sin(4θ)]_0 ^(π/2) =(π/(48)) −0 ⇒ I= (π/(48)) .](https://www.tinkutara.com/question/Q28453.png)
$${I}=\:\frac{\pi}{\mathrm{48}}\:−\frac{\mathrm{1}}{\mathrm{24}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}\left(\mathrm{4}\theta\right){d}\theta=\:\frac{\pi}{\mathrm{48}}\:\:−\:\frac{\mathrm{1}}{\mathrm{4}×\mathrm{24}}\left[{sin}\left(\mathrm{4}\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\frac{\pi}{\mathrm{48}}\:−\mathrm{0} \\ $$$$\Rightarrow\:\:{I}=\:\frac{\pi}{\mathrm{48}}\:. \\ $$
