Question Number 158049 by zainaltanjung last updated on 30/Oct/21
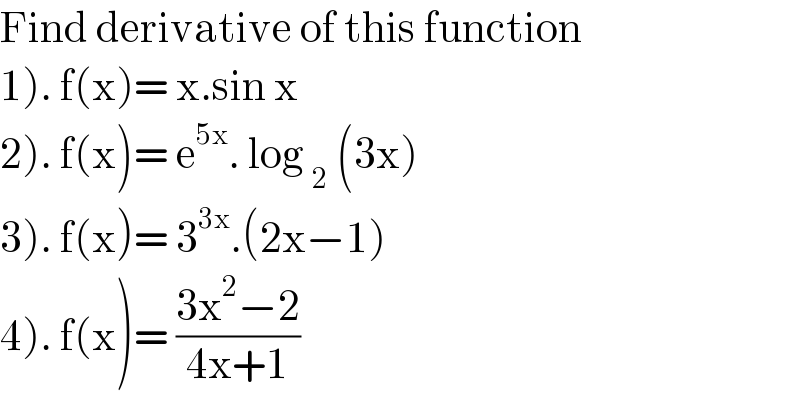
$$\mathrm{Find}\:\mathrm{derivative}\:\mathrm{of}\:\mathrm{this}\:\mathrm{function} \\ $$$$\left.\mathrm{1}\right).\:\mathrm{f}\left(\mathrm{x}\right)=\:\mathrm{x}.\mathrm{sin}\:\mathrm{x} \\ $$$$\left.\mathrm{2}\right).\:\mathrm{f}\left(\mathrm{x}\right)=\:\mathrm{e}^{\mathrm{5x}} .\:\mathrm{log}\:_{\mathrm{2}} \:\left(\mathrm{3x}\right) \\ $$$$\left.\mathrm{3}\right).\:\mathrm{f}\left(\mathrm{x}\right)=\:\mathrm{3}^{\mathrm{3x}} .\left(\mathrm{2x}−\mathrm{1}\right) \\ $$$$\left.\mathrm{4}\right).\:\mathrm{f}\left(\mathrm{x}\right)=\:\frac{\mathrm{3x}^{\mathrm{2}} −\mathrm{2}}{\mathrm{4x}+\mathrm{1}} \\ $$
Answered by MathsFan last updated on 30/Oct/21
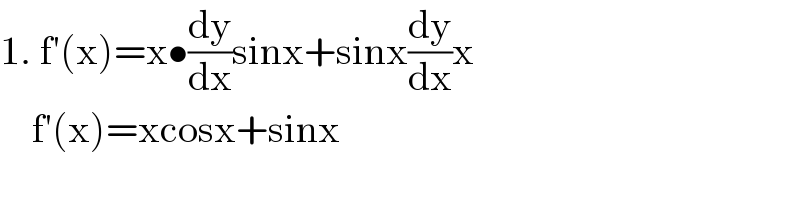
$$\mathrm{1}.\:\mathrm{f}'\left(\mathrm{x}\right)=\mathrm{x}\bullet\frac{\mathrm{dy}}{\mathrm{dx}}\mathrm{sinx}+\mathrm{sinx}\frac{\mathrm{dy}}{\mathrm{dx}}\mathrm{x} \\ $$$$\:\:\:\:\mathrm{f}'\left(\mathrm{x}\right)=\mathrm{xcosx}+\mathrm{sinx} \\ $$
Answered by MathsFan last updated on 30/Oct/21
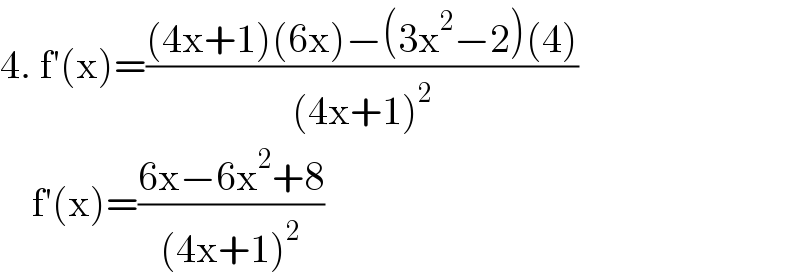
$$\mathrm{4}.\:\mathrm{f}'\left(\mathrm{x}\right)=\frac{\left(\mathrm{4x}+\mathrm{1}\right)\left(\mathrm{6x}\right)−\left(\mathrm{3x}^{\mathrm{2}} −\mathrm{2}\right)\left(\mathrm{4}\right)}{\left(\mathrm{4x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\mathrm{f}'\left(\mathrm{x}\right)=\frac{\mathrm{6x}−\mathrm{6x}^{\mathrm{2}} +\mathrm{8}}{\left(\mathrm{4x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$
