Question Number 16701 by Tinkutara last updated on 25/Jun/17
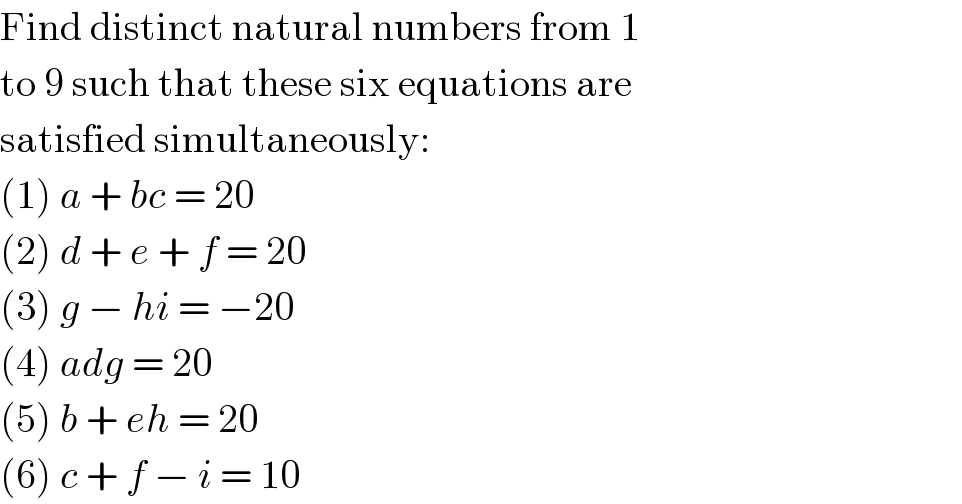
$$\mathrm{Find}\:\mathrm{distinct}\:\mathrm{natural}\:\mathrm{numbers}\:\mathrm{from}\:\mathrm{1} \\ $$$$\mathrm{to}\:\mathrm{9}\:\mathrm{such}\:\mathrm{that}\:\mathrm{these}\:\mathrm{six}\:\mathrm{equations}\:\mathrm{are} \\ $$$$\mathrm{satisfied}\:\mathrm{simultaneously}: \\ $$$$\left(\mathrm{1}\right)\:{a}\:+\:{bc}\:=\:\mathrm{20} \\ $$$$\left(\mathrm{2}\right)\:{d}\:+\:{e}\:+\:{f}\:=\:\mathrm{20} \\ $$$$\left(\mathrm{3}\right)\:{g}\:−\:{hi}\:=\:−\mathrm{20} \\ $$$$\left(\mathrm{4}\right)\:{adg}\:=\:\mathrm{20} \\ $$$$\left(\mathrm{5}\right)\:{b}\:+\:{eh}\:=\:\mathrm{20} \\ $$$$\left(\mathrm{6}\right)\:{c}\:+\:{f}\:−\:{i}\:=\:\mathrm{10} \\ $$
Answered by RasheedSoomro last updated on 26/Jun/17
![{a,b,c,d,e,f,g,h,i}={1,2,3,4,5,6,7,8,9} adg=20=1×4×5 [Only one way disregard to order] ∴ {a,d,g}={1,4,5}........................(i) ∴{b,c,e,f,h,i}={2,3,6,7,8,9} { ((a=1⇒a+bc=20⇒bc=19 ≠(1≤x≤9)×(1≤y≤9), ∴a≠1)),((a=4⇒bc=16=2×8⇒{b,c}={2,8})),((a=5⇒bc=15=3×5 but b∣c≠5 because a=5)) :} So, surely a=4 ∧ {b,c}={2,8} ∴ {e,f,h,i}={3,6,7,9} { ((g≠4 because a=4)),((g=1⇒hi−g=20⇒hi=21=3×7⇒{h,i}={3,7})),((g=5⇒hi=25=5×5 but {g,h,i}≠{5,5,5})) :} So, surely g=1 ∧ {h,i}={3,7} ∴ {e,f}={6,9} { ((b=2⇒b+eh=20⇒eh=18=3×6 ⇒{e,h}={3,6})),((b=8⇒eh=12^• )) :} ^• 12 can be 2×6 or 3×4 but these values are assigned to others {a,d,g}={1,4,5},a=4,g=1⇒d=5 {: (({h,i}={3,7})),(({e,h}={3,6})),(({e,f}={6,9})) }⇒h=3,i=7,e=6,f=9 {b,c}={2,8} { ((c+f−i=10⇒c+9−7=10⇒c=8)),(({b,c}={2,8}∧c=8⇒b=2)) :} a=4,b=2,c=8,d=5,e=6,f=9,g=1,h=3,i=7](https://www.tinkutara.com/question/Q16715.png)
$$\left\{\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d},\mathrm{e},\mathrm{f},\mathrm{g},\mathrm{h},\mathrm{i}\right\}=\left\{\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5},\mathrm{6},\mathrm{7},\mathrm{8},\mathrm{9}\right\} \\ $$$$\mathrm{adg}=\mathrm{20}=\mathrm{1}×\mathrm{4}×\mathrm{5}\:\:\left[\mathrm{Only}\:\mathrm{one}\:\mathrm{way}\:\mathrm{disregard}\:\mathrm{to}\:\mathrm{order}\right] \\ $$$$\therefore\:\:\left\{\mathrm{a},\mathrm{d},\mathrm{g}\right\}=\left\{\mathrm{1},\mathrm{4},\mathrm{5}\right\}……………………\left(\mathrm{i}\right) \\ $$$$\therefore\left\{\mathrm{b},\mathrm{c},\mathrm{e},\mathrm{f},\mathrm{h},\mathrm{i}\right\}=\left\{\mathrm{2},\mathrm{3},\mathrm{6},\mathrm{7},\mathrm{8},\mathrm{9}\right\} \\ $$$$\begin{cases}{\mathrm{a}=\mathrm{1}\Rightarrow\mathrm{a}+\mathrm{bc}=\mathrm{20}\Rightarrow\mathrm{bc}=\mathrm{19}\:\neq\left(\mathrm{1}\leqslant\mathrm{x}\leqslant\mathrm{9}\right)×\left(\mathrm{1}\leqslant\mathrm{y}\leqslant\mathrm{9}\right),\:\therefore\mathrm{a}\neq\mathrm{1}}\\{\mathrm{a}=\mathrm{4}\Rightarrow\mathrm{bc}=\mathrm{16}=\mathrm{2}×\mathrm{8}\Rightarrow\left\{\mathrm{b},\mathrm{c}\right\}=\left\{\mathrm{2},\mathrm{8}\right\}}\\{\mathrm{a}=\mathrm{5}\Rightarrow\mathrm{bc}=\mathrm{15}=\mathrm{3}×\mathrm{5}\:\mathrm{but}\:\mathrm{b}\mid\mathrm{c}\neq\mathrm{5}\:\mathrm{because}\:\mathrm{a}=\mathrm{5}}\end{cases} \\ $$$$\mathrm{So},\:\mathrm{surely}\:\mathrm{a}=\mathrm{4}\:\wedge\:\left\{\mathrm{b},\mathrm{c}\right\}=\left\{\mathrm{2},\mathrm{8}\right\} \\ $$$$\therefore\:\left\{\mathrm{e},\mathrm{f},\mathrm{h},\mathrm{i}\right\}=\left\{\mathrm{3},\mathrm{6},\mathrm{7},\mathrm{9}\right\} \\ $$$$\begin{cases}{\mathrm{g}\neq\mathrm{4}\:\mathrm{because}\:\mathrm{a}=\mathrm{4}}\\{\mathrm{g}=\mathrm{1}\Rightarrow\mathrm{hi}−\mathrm{g}=\mathrm{20}\Rightarrow\mathrm{hi}=\mathrm{21}=\mathrm{3}×\mathrm{7}\Rightarrow\left\{\mathrm{h},\mathrm{i}\right\}=\left\{\mathrm{3},\mathrm{7}\right\}}\\{\mathrm{g}=\mathrm{5}\Rightarrow\mathrm{hi}=\mathrm{25}=\mathrm{5}×\mathrm{5}\:\mathrm{but}\:\left\{\mathrm{g},\mathrm{h},\mathrm{i}\right\}\neq\left\{\mathrm{5},\mathrm{5},\mathrm{5}\right\}}\end{cases} \\ $$$$\mathrm{So},\:\mathrm{surely}\:\mathrm{g}=\mathrm{1}\:\wedge\:\left\{\mathrm{h},\mathrm{i}\right\}=\left\{\mathrm{3},\mathrm{7}\right\} \\ $$$$\therefore\:\left\{\mathrm{e},\mathrm{f}\right\}=\left\{\mathrm{6},\mathrm{9}\right\} \\ $$$$\begin{cases}{\mathrm{b}=\mathrm{2}\Rightarrow\mathrm{b}+\mathrm{eh}=\mathrm{20}\Rightarrow\mathrm{eh}=\mathrm{18}=\mathrm{3}×\mathrm{6}\:\Rightarrow\left\{\mathrm{e},\mathrm{h}\right\}=\left\{\mathrm{3},\mathrm{6}\right\}}\\{\mathrm{b}=\mathrm{8}\Rightarrow\mathrm{eh}=\mathrm{12}^{\bullet} }\end{cases} \\ $$$$\:^{\bullet} \mathrm{12}\:\mathrm{can}\:\mathrm{be}\:\mathrm{2}×\mathrm{6}\:\mathrm{or}\:\mathrm{3}×\mathrm{4}\:\mathrm{but}\:\mathrm{these}\:\mathrm{values}\:\mathrm{are}\:\mathrm{assigned}\:\mathrm{to}\:\mathrm{others} \\ $$$$\left\{\mathrm{a},\mathrm{d},\mathrm{g}\right\}=\left\{\mathrm{1},\mathrm{4},\mathrm{5}\right\},\mathrm{a}=\mathrm{4},\mathrm{g}=\mathrm{1}\Rightarrow\mathrm{d}=\mathrm{5} \\ $$$$\left.\begin{matrix}{\left\{\mathrm{h},\mathrm{i}\right\}=\left\{\mathrm{3},\mathrm{7}\right\}}\\{\left\{\mathrm{e},\mathrm{h}\right\}=\left\{\mathrm{3},\mathrm{6}\right\}}\\{\left\{\mathrm{e},\mathrm{f}\right\}=\left\{\mathrm{6},\mathrm{9}\right\}}\end{matrix}\right\}\Rightarrow\mathrm{h}=\mathrm{3},\mathrm{i}=\mathrm{7},\mathrm{e}=\mathrm{6},\mathrm{f}=\mathrm{9} \\ $$$$\left\{\mathrm{b},\mathrm{c}\right\}=\left\{\mathrm{2},\mathrm{8}\right\} \\ $$$$\begin{cases}{\mathrm{c}+\mathrm{f}−\mathrm{i}=\mathrm{10}\Rightarrow\mathrm{c}+\mathrm{9}−\mathrm{7}=\mathrm{10}\Rightarrow\mathrm{c}=\mathrm{8}}\\{\left\{\mathrm{b},\mathrm{c}\right\}=\left\{\mathrm{2},\mathrm{8}\right\}\wedge\mathrm{c}=\mathrm{8}\Rightarrow\mathrm{b}=\mathrm{2}}\end{cases} \\ $$$$\mathrm{a}=\mathrm{4},\mathrm{b}=\mathrm{2},\mathrm{c}=\mathrm{8},\mathrm{d}=\mathrm{5},\mathrm{e}=\mathrm{6},\mathrm{f}=\mathrm{9},\mathrm{g}=\mathrm{1},\mathrm{h}=\mathrm{3},\mathrm{i}=\mathrm{7} \\ $$
Commented by Tinkutara last updated on 26/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
