Question Number 83917 by turbo msup by abdo last updated on 07/Mar/20
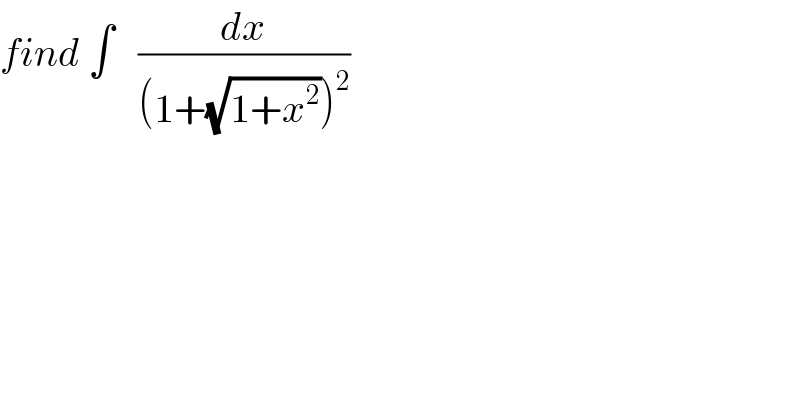
$${find}\:\int\:\:\:\frac{{dx}}{\left(\mathrm{1}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} } \\ $$
Answered by redmiiuser last updated on 08/Mar/20

Answered by redmiiuser last updated on 08/Mar/20

Answered by redmiiuser last updated on 08/Mar/20

Answered by M±th+et£s last updated on 08/Mar/20
![let x=tan(t) t=tan^(−1) (x) dx=sec^2 (t) ∫(1/((1+(√(1+tan^2 (t))))^2 )) sec^2 (t) dt ∫(1/((1+sec(t))^2 ))sec^2 (t) dt ∫(1/((1+(1/(cos(t))))^2 )) sec^2 (t) dt ∫(1/((cos(t)+1)^2 ))dt⇒∫(1/((2cos^2 ((t/2)))^2 ))dt (1/4)∫sec^4 ((t/2)) dt (1/4)∫(tan^2 ((t/2))+1)sec^2 ((t/2))dt (1/4)[∫tan^2 ((t/2))sec^2 ((t/2)) dt] +[∫sec^2 ((t/2))dt] ((tan^3 ((t/2)))/6)+((tan(t/2))/2)+c (1/6) tan(((tan^(−1) (x))/2))+(1/2)tan(((tan^(−1) (x))/2))+c](https://www.tinkutara.com/question/Q83945.png)
$${let}\:{x}={tan}\left({t}\right)\:\:\:\:\:{t}={tan}^{−\mathrm{1}} \left({x}\right) \\ $$$${dx}={sec}^{\mathrm{2}} \left({t}\right) \\ $$$$\int\frac{\mathrm{1}}{\left(\mathrm{1}+\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \left({t}\right)}\right)^{\mathrm{2}} }\:{sec}^{\mathrm{2}} \left({t}\right)\:{dt} \\ $$$$\int\frac{\mathrm{1}}{\left(\mathrm{1}+{sec}\left({t}\right)\right)^{\mathrm{2}} }{sec}^{\mathrm{2}} \left({t}\right)\:{dt} \\ $$$$\int\frac{\mathrm{1}}{\left(\mathrm{1}+\frac{\mathrm{1}}{{cos}\left({t}\right)}\right)^{\mathrm{2}} }\:{sec}^{\mathrm{2}} \left({t}\right)\:{dt} \\ $$$$\int\frac{\mathrm{1}}{\left({cos}\left({t}\right)+\mathrm{1}\right)^{\mathrm{2}} }{dt}\Rightarrow\int\frac{\mathrm{1}}{\left(\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{{t}}{\mathrm{2}}\right)\right)^{\mathrm{2}} }{dt} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int{sec}^{\mathrm{4}} \left(\frac{{t}}{\mathrm{2}}\right)\:{dt} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int\left({tan}^{\mathrm{2}} \left(\frac{{t}}{\mathrm{2}}\right)+\mathrm{1}\right){sec}^{\mathrm{2}} \left(\frac{{t}}{\mathrm{2}}\right){dt} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\left[\int{tan}^{\mathrm{2}} \left(\frac{{t}}{\mathrm{2}}\right){sec}^{\mathrm{2}} \left(\frac{{t}}{\mathrm{2}}\right)\:{dt}\right]\:+\left[\int{sec}^{\mathrm{2}} \left(\frac{{t}}{\mathrm{2}}\right){dt}\right] \\ $$$$\frac{{tan}^{\mathrm{3}} \left(\frac{{t}}{\mathrm{2}}\right)}{\mathrm{6}}+\frac{{tan}\frac{{t}}{\mathrm{2}}}{\mathrm{2}}+{c} \\ $$$$\frac{\mathrm{1}}{\mathrm{6}}\:{tan}\left(\frac{{tan}^{−\mathrm{1}} \left({x}\right)}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}{tan}\left(\frac{{tan}^{−\mathrm{1}} \left({x}\right)}{\mathrm{2}}\right)+{c} \\ $$
Commented by redmiiuser last updated on 08/Mar/20

$${Both}\:{of}\:{us}\:{got}\:{the} \\ $$$${same}\:{answer}.{But}\: \\ $$$${you}\:{are}\:{a}\:{bit}\:{more}\: \\ $$$${intelligent}\:{than}\:{me} \\ $$$${at}\:{the}\:{last}\:{step}. \\ $$
Answered by M±th+et£s last updated on 09/Mar/20
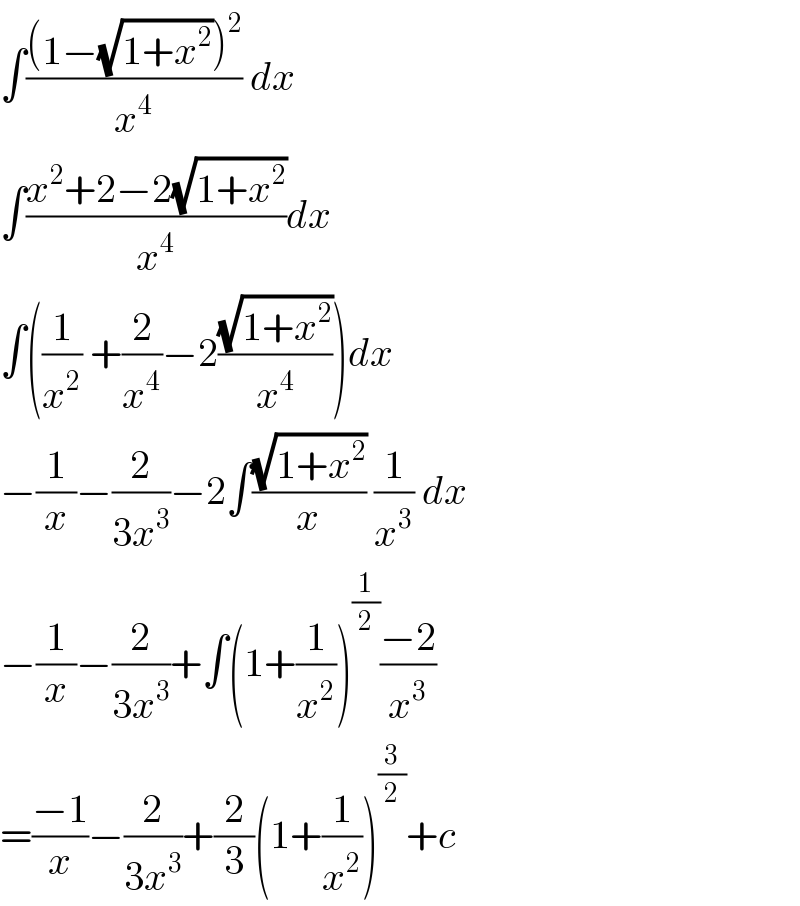
$$\int\frac{\left(\mathrm{1}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} }{{x}^{\mathrm{4}} }\:{dx} \\ $$$$\int\frac{{x}^{\mathrm{2}} +\mathrm{2}−\mathrm{2}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}^{\mathrm{4}} }{dx} \\ $$$$\int\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:+\frac{\mathrm{2}}{{x}^{\mathrm{4}} }−\mathrm{2}\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}^{\mathrm{4}} }\right){dx} \\ $$$$−\frac{\mathrm{1}}{{x}}−\frac{\mathrm{2}}{\mathrm{3}{x}^{\mathrm{3}} }−\mathrm{2}\int\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}}\:\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\:{dx} \\ $$$$−\frac{\mathrm{1}}{{x}}−\frac{\mathrm{2}}{\mathrm{3}{x}^{\mathrm{3}} }+\int\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{−\mathrm{2}}{{x}^{\mathrm{3}} } \\ $$$$=\frac{−\mathrm{1}}{{x}}−\frac{\mathrm{2}}{\mathrm{3}{x}^{\mathrm{3}} }+\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +{c} \\ $$
