Question Number 36421 by abdo.msup.com last updated on 01/Jun/18
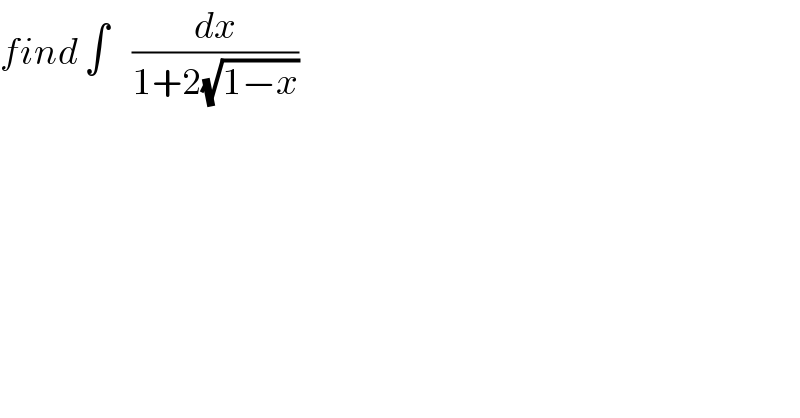
$${find}\:\int\:\:\:\:\frac{{dx}}{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{1}−{x}}} \\ $$
Commented by abdo.msup.com last updated on 04/Jun/18
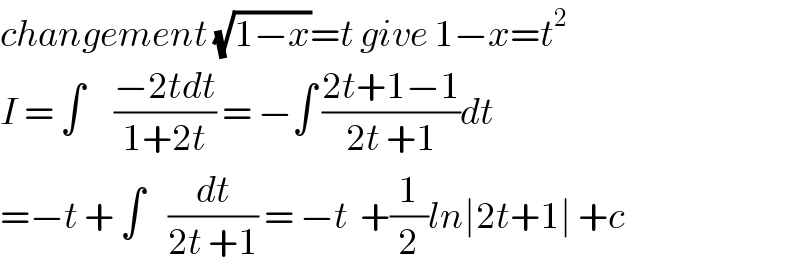
$${changement}\:\sqrt{\mathrm{1}−{x}}={t}\:{give}\:\mathrm{1}−{x}={t}^{\mathrm{2}} \\ $$$${I}\:=\:\int\:\:\:\:\:\frac{−\mathrm{2}{tdt}}{\mathrm{1}+\mathrm{2}{t}}\:=\:−\int\:\frac{\mathrm{2}{t}+\mathrm{1}−\mathrm{1}}{\mathrm{2}{t}\:+\mathrm{1}}{dt} \\ $$$$=−{t}\:+\:\int\:\:\:\:\frac{{dt}}{\mathrm{2}{t}\:+\mathrm{1}}\:=\:−{t}\:\:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\mathrm{2}{t}+\mathrm{1}\mid\:+{c} \\ $$
