Menu Close

find-dx-1-chx-2-2-calculate-0-1-dx-1-chx-2-

Tinku Tara 0 Comments
Pin




Question Number 34285 by math khazana by abdo last updated on 03/May/18
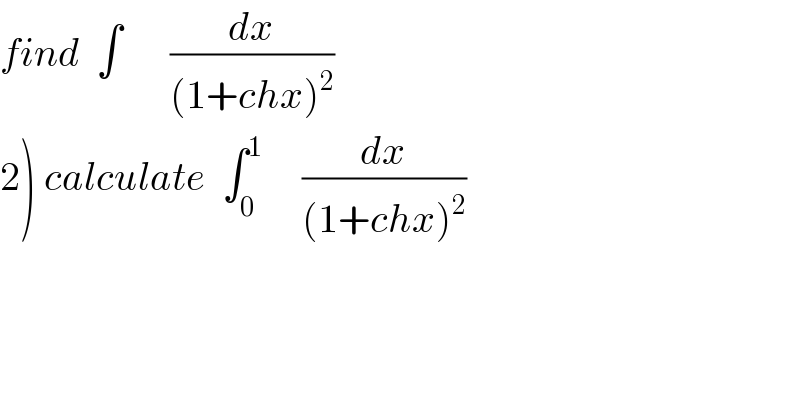
find ∫ (dx/((1+chx)^2 )) 2) calculate ∫_0 ^1 (dx/((1+chx)^2 ))
$${find}\:\:\int\:\:\:\:\:\:\frac{{dx}}{\left(\mathrm{1}+{chx}\right)^{\mathrm{2}} } \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\frac{{dx}}{\left(\mathrm{1}+{chx}\right)^{\mathrm{2}} } \\ $$
Commented by prof Abdo imad last updated on 06/May/18
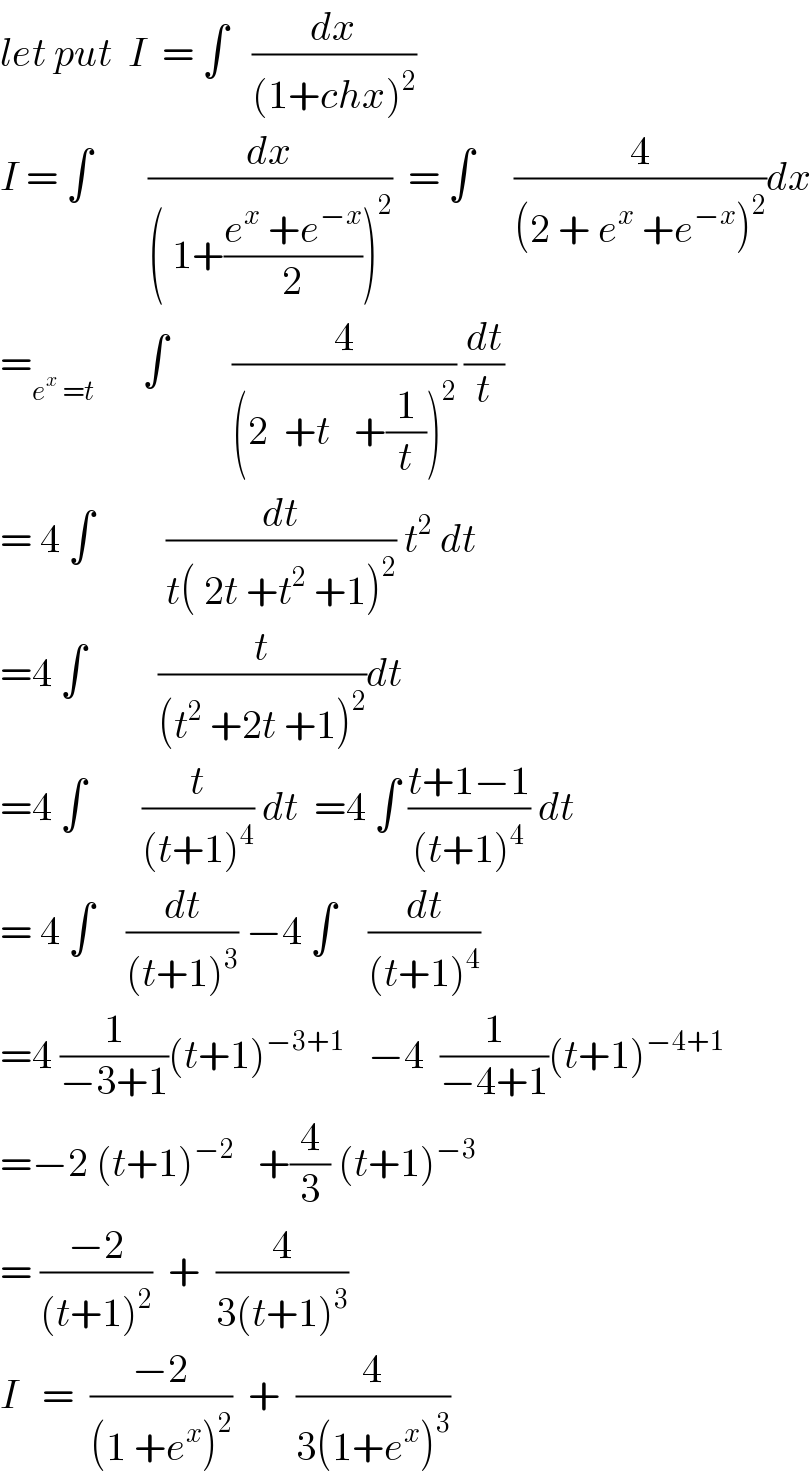
let put I = ∫ (dx/((1+chx)^2 )) I = ∫ (dx/(( 1+((e^x +e^(−x) )/2))^2 )) = ∫ (4/((2 + e^x +e^(−x) )^2 ))dx =_(e^x =t) ∫ (4/((2 +t +(1/t))^2 )) (dt/t) = 4 ∫ (dt/(t( 2t +t^2 +1)^2 )) t^2 dt =4 ∫ (t/((t^2 +2t +1)^2 ))dt =4 ∫ (t/((t+1)^4 )) dt =4 ∫ ((t+1−1)/((t+1)^4 )) dt = 4 ∫ (dt/((t+1)^3 )) −4 ∫ (dt/((t+1)^4 )) =4 (1/(−3+1))(t+1)^(−3+1) −4 (1/(−4+1))(t+1)^(−4+1) =−2 (t+1)^(−2) +(4/3) (t+1)^(−3) = ((−2)/((t+1)^2 )) + (4/(3(t+1)^3 )) I = ((−2)/((1 +e^x )^2 )) + (4/(3(1+e^x )^3 ))
$${let}\:{put}\:\:{I}\:\:=\:\int\:\:\:\frac{{dx}}{\left(\mathrm{1}+{chx}\right)^{\mathrm{2}} } \\ $$$${I}\:=\:\int\:\:\:\:\:\:\:\frac{{dx}}{\left(\:\mathrm{1}+\frac{{e}^{{x}} \:+{e}^{−{x}} }{\mathrm{2}}\right)^{\mathrm{2}} }\:\:=\:\int\:\:\:\:\:\frac{\mathrm{4}}{\left(\mathrm{2}\:+\:{e}^{{x}} \:+{e}^{−{x}} \right)^{\mathrm{2}} }{dx} \\ $$$$=_{{e}^{{x}} \:={t}} \:\:\:\:\:\:\int\:\:\:\:\:\:\:\:\frac{\mathrm{4}}{\left(\mathrm{2}\:\:+{t}\:\:\:+\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} }\:\frac{{dt}}{{t}} \\ $$$$=\:\mathrm{4}\:\int\:\:\:\:\:\:\:\:\:\frac{{dt}}{{t}\left(\:\mathrm{2}{t}\:+{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:{t}^{\mathrm{2}} \:{dt} \\ $$$$=\mathrm{4}\:\int\:\:\:\:\:\:\:\:\:\frac{{t}}{\left({t}^{\mathrm{2}} \:+\mathrm{2}{t}\:+\mathrm{1}\right)^{\mathrm{2}} }{dt} \\ $$$$=\mathrm{4}\:\int\:\:\:\:\:\:\:\frac{{t}}{\left({t}+\mathrm{1}\right)^{\mathrm{4}} }\:{dt}\:\:=\mathrm{4}\:\int\:\frac{{t}+\mathrm{1}−\mathrm{1}}{\left({t}+\mathrm{1}\right)^{\mathrm{4}} }\:{dt} \\ $$$$=\:\mathrm{4}\:\int\:\:\:\:\frac{{dt}}{\left({t}+\mathrm{1}\right)^{\mathrm{3}} }\:−\mathrm{4}\:\int\:\:\:\:\frac{{dt}}{\left({t}+\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$=\mathrm{4}\:\frac{\mathrm{1}}{−\mathrm{3}+\mathrm{1}}\left({t}+\mathrm{1}\right)^{−\mathrm{3}+\mathrm{1}} \:\:\:−\mathrm{4}\:\:\frac{\mathrm{1}}{−\mathrm{4}+\mathrm{1}}\left({t}+\mathrm{1}\right)^{−\mathrm{4}+\mathrm{1}} \\ $$$$=−\mathrm{2}\:\left({t}+\mathrm{1}\right)^{−\mathrm{2}} \:\:\:+\frac{\mathrm{4}}{\mathrm{3}}\:\left({t}+\mathrm{1}\right)^{−\mathrm{3}} \\ $$$$=\:\frac{−\mathrm{2}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }\:\:+\:\:\frac{\mathrm{4}}{\mathrm{3}\left({t}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$${I}\:\:\:=\:\:\frac{−\mathrm{2}}{\left(\mathrm{1}\:+{e}^{{x}} \right)^{\mathrm{2}} }\:\:+\:\:\frac{\mathrm{4}}{\mathrm{3}\left(\mathrm{1}+{e}^{{x}} \right)^{\mathrm{3}} } \\ $$
Commented by prof Abdo imad last updated on 06/May/18
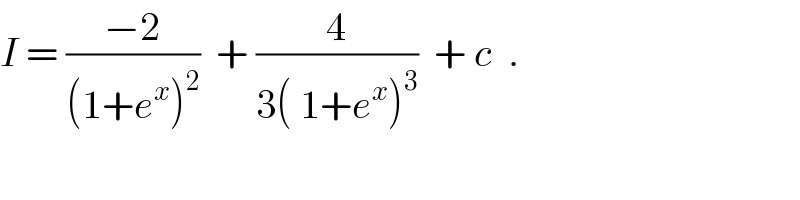
I = ((−2)/((1+e^x )^2 )) + (4/(3( 1+e^x )^3 )) + c .
$${I}\:=\:\frac{−\mathrm{2}}{\left(\mathrm{1}+{e}^{{x}} \right)^{\mathrm{2}} }\:\:+\:\frac{\mathrm{4}}{\mathrm{3}\left(\:\mathrm{1}+{e}^{{x}} \right)^{\mathrm{3}} }\:\:+\:{c}\:\:. \\ $$
Commented by prof Abdo imad last updated on 06/May/18
∫_0 ^1 (dx/((1+chx)^2 )) =[ (4/(3(1+e^x )^3 )) −(2/((1+e^x )^2 ))]_0 ^1 = (4/(3(1+e)^3 )) −(2/((1 +e)^2 )) −(4/(3.8)) +(2/2^2 ) = (4/(3( 1+e)^3 )) −(2/((1+e)^2 )) −(1/6) +(1/2) = (4/(3(1+e)^3 )) −(2/((1+e)^2 )) +(1/3) .
$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\:\frac{{dx}}{\left(\mathrm{1}+{chx}\right)^{\mathrm{2}} }\:\:=\left[\:\:\frac{\mathrm{4}}{\mathrm{3}\left(\mathrm{1}+{e}^{{x}} \right)^{\mathrm{3}} }\:−\frac{\mathrm{2}}{\left(\mathrm{1}+{e}^{{x}} \right)^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\:\frac{\mathrm{4}}{\mathrm{3}\left(\mathrm{1}+{e}\right)^{\mathrm{3}} }\:−\frac{\mathrm{2}}{\left(\mathrm{1}\:+{e}\right)^{\mathrm{2}} }\:−\frac{\mathrm{4}}{\mathrm{3}.\mathrm{8}}\:+\frac{\mathrm{2}}{\mathrm{2}^{\mathrm{2}} } \\ $$$$=\:\frac{\mathrm{4}}{\mathrm{3}\left(\:\mathrm{1}+{e}\right)^{\mathrm{3}} }\:−\frac{\mathrm{2}}{\left(\mathrm{1}+{e}\right)^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{6}}\:+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$=\:\frac{\mathrm{4}}{\mathrm{3}\left(\mathrm{1}+{e}\right)^{\mathrm{3}} }\:−\frac{\mathrm{2}}{\left(\mathrm{1}+{e}\right)^{\mathrm{2}} }\:\:+\frac{\mathrm{1}}{\mathrm{3}}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *