Menu Close

find-dx-1-cosx-cos-2x-

Tinku Tara 0 Comments
Pin




Question Number 64818 by mathmax by abdo last updated on 22/Jul/19
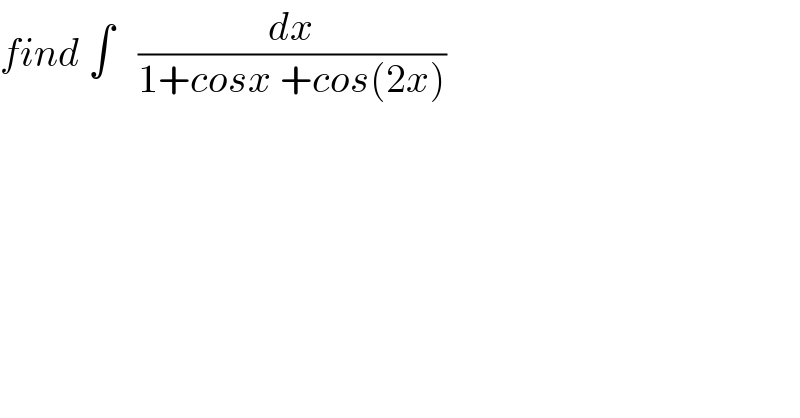
find ∫ (dx/(1+cosx +cos(2x)))
$${find}\:\int\:\:\:\frac{{dx}}{\mathrm{1}+{cosx}\:+{cos}\left(\mathrm{2}{x}\right)} \\ $$
Commented by mathmax by abdo last updated on 22/Jul/19
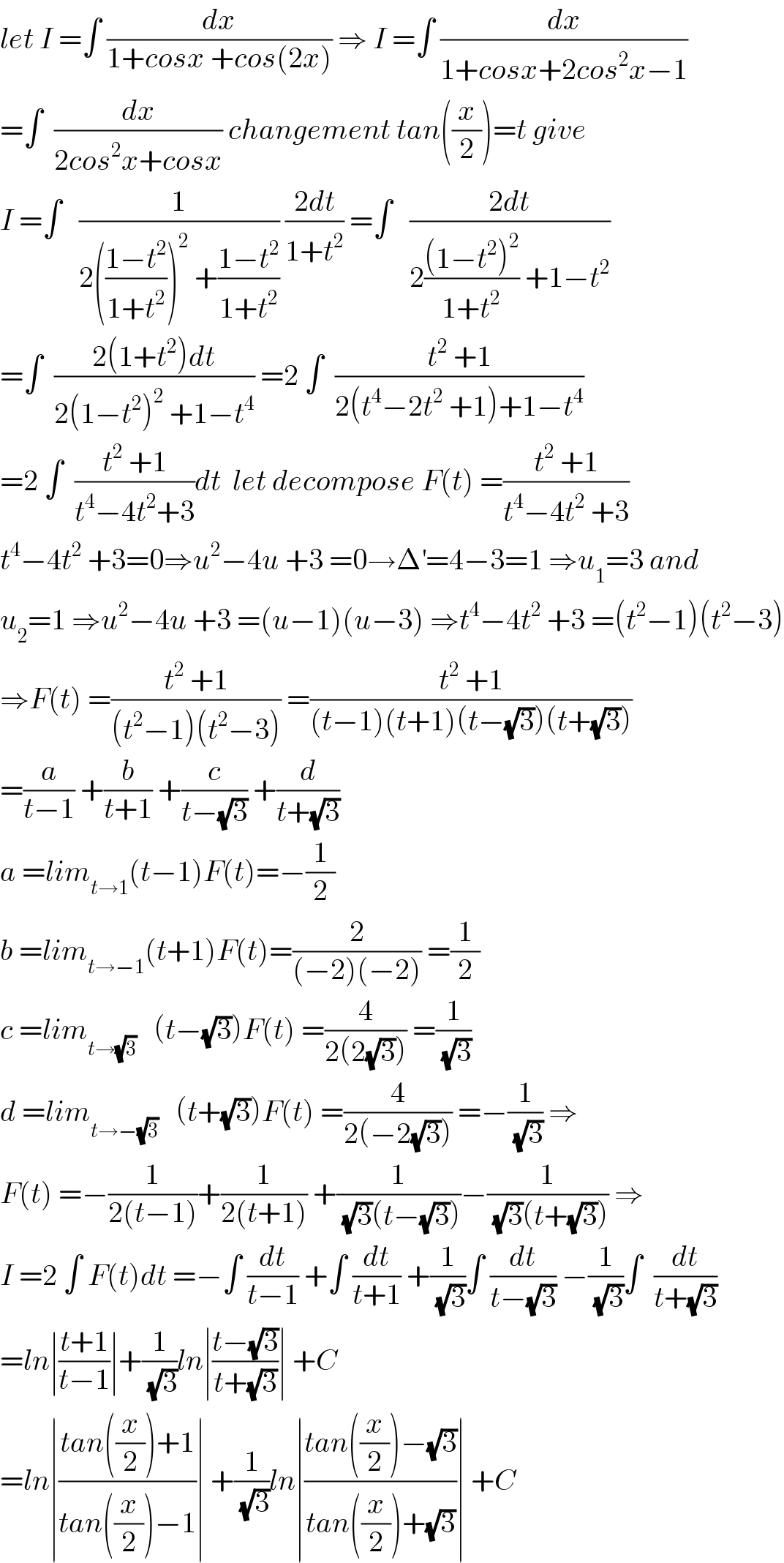
let I =∫ (dx/(1+cosx +cos(2x))) ⇒ I =∫ (dx/(1+cosx+2cos^2 x−1)) =∫ (dx/(2cos^2 x+cosx)) changement tan((x/2))=t give I =∫ (1/(2(((1−t^2 )/(1+t^2 )))^2 +((1−t^2 )/(1+t^2 )))) ((2dt)/(1+t^2 )) =∫ ((2dt)/(2(((1−t^2 )^2 )/(1+t^2 )) +1−t^2 )) =∫ ((2(1+t^2 )dt)/(2(1−t^2 )^2 +1−t^4 )) =2 ∫ ((t^2 +1)/(2(t^4 −2t^2 +1)+1−t^4 )) =2 ∫ ((t^2 +1)/(t^4 −4t^2 +3))dt let decompose F(t) =((t^2 +1)/(t^4 −4t^2 +3)) t^4 −4t^2 +3=0⇒u^2 −4u +3 =0→Δ^′ =4−3=1 ⇒u_1 =3 and u_2 =1 ⇒u^2 −4u +3 =(u−1)(u−3) ⇒t^4 −4t^2 +3 =(t^2 −1)(t^2 −3) ⇒F(t) =((t^2 +1)/((t^2 −1)(t^2 −3))) =((t^2 +1)/((t−1)(t+1)(t−(√3))(t+(√3)))) =(a/(t−1)) +(b/(t+1)) +(c/(t−(√3))) +(d/(t+(√3))) a =lim_(t→1) (t−1)F(t)=−(1/2) b =lim_(t→−1) (t+1)F(t)=(2/((−2)(−2))) =(1/2) c =lim_(t→(√3)) (t−(√3))F(t) =(4/(2(2(√3)))) =(1/( (√3))) d =lim_(t→−(√3)) (t+(√3))F(t) =(4/(2(−2(√3)))) =−(1/( (√3))) ⇒ F(t) =−(1/(2(t−1)))+(1/(2(t+1))) +(1/( (√3)(t−(√3))))−(1/( (√3)(t+(√3)))) ⇒ I =2 ∫ F(t)dt =−∫ (dt/(t−1)) +∫ (dt/(t+1)) +(1/( (√3)))∫ (dt/(t−(√3))) −(1/( (√3)))∫ (dt/(t+(√3))) =ln∣((t+1)/(t−1))∣+(1/( (√3)))ln∣((t−(√3))/(t+(√3)))∣ +C =ln∣((tan((x/2))+1)/(tan((x/2))−1))∣ +(1/( (√3)))ln∣((tan((x/2))−(√3))/(tan((x/2))+(√3)))∣ +C
$${let}\:{I}\:=\int\:\frac{{dx}}{\mathrm{1}+{cosx}\:+{cos}\left(\mathrm{2}{x}\right)}\:\Rightarrow\:{I}\:=\int\:\frac{{dx}}{\mathrm{1}+{cosx}+\mathrm{2}{cos}^{\mathrm{2}} {x}−\mathrm{1}} \\ $$$$=\int\:\:\frac{{dx}}{\mathrm{2}{cos}^{\mathrm{2}} {x}+{cosx}}\:{changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give} \\ $$$${I}\:=\int\:\:\:\frac{\mathrm{1}}{\mathrm{2}\left(\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)^{\mathrm{2}} \:+\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\int\:\:\:\frac{\mathrm{2}{dt}}{\mathrm{2}\frac{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:+\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$$=\int\:\:\frac{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{2}} \right){dt}}{\mathrm{2}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} \:+\mathrm{1}−{t}^{\mathrm{4}} }\:=\mathrm{2}\:\int\:\:\frac{{t}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{2}\left({t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}\right)+\mathrm{1}−{t}^{\mathrm{4}} } \\ $$$$=\mathrm{2}\:\int\:\:\frac{{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}^{\mathrm{4}} −\mathrm{4}{t}^{\mathrm{2}} +\mathrm{3}}{dt}\:\:{let}\:{decompose}\:{F}\left({t}\right)\:=\frac{{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}^{\mathrm{4}} −\mathrm{4}{t}^{\mathrm{2}} \:+\mathrm{3}} \\ $$$${t}^{\mathrm{4}} −\mathrm{4}{t}^{\mathrm{2}} \:+\mathrm{3}=\mathrm{0}\Rightarrow{u}^{\mathrm{2}} −\mathrm{4}{u}\:+\mathrm{3}\:=\mathrm{0}\rightarrow\Delta^{'} =\mathrm{4}−\mathrm{3}=\mathrm{1}\:\Rightarrow{u}_{\mathrm{1}} =\mathrm{3}\:{and} \\ $$$${u}_{\mathrm{2}} =\mathrm{1}\:\Rightarrow{u}^{\mathrm{2}} −\mathrm{4}{u}\:+\mathrm{3}\:=\left({u}−\mathrm{1}\right)\left({u}−\mathrm{3}\right)\:\Rightarrow{t}^{\mathrm{4}} −\mathrm{4}{t}^{\mathrm{2}} \:+\mathrm{3}\:=\left({t}^{\mathrm{2}} −\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{3}\right) \\ $$$$\Rightarrow{F}\left({t}\right)\:=\frac{{t}^{\mathrm{2}} \:+\mathrm{1}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{3}\right)}\:=\frac{{t}^{\mathrm{2}} \:+\mathrm{1}}{\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)\left({t}−\sqrt{\mathrm{3}}\right)\left({t}+\sqrt{\mathrm{3}}\right)} \\ $$$$=\frac{{a}}{{t}−\mathrm{1}}\:+\frac{{b}}{{t}+\mathrm{1}}\:+\frac{{c}}{{t}−\sqrt{\mathrm{3}}}\:+\frac{{d}}{{t}+\sqrt{\mathrm{3}}} \\ $$$${a}\:={lim}_{{t}\rightarrow\mathrm{1}} \left({t}−\mathrm{1}\right){F}\left({t}\right)=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${b}\:={lim}_{{t}\rightarrow−\mathrm{1}} \left({t}+\mathrm{1}\right){F}\left({t}\right)=\frac{\mathrm{2}}{\left(−\mathrm{2}\right)\left(−\mathrm{2}\right)}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${c}\:={lim}_{{t}\rightarrow\sqrt{\mathrm{3}}} \:\:\:\left({t}−\sqrt{\mathrm{3}}\right){F}\left({t}\right)\:=\frac{\mathrm{4}}{\mathrm{2}\left(\mathrm{2}\sqrt{\mathrm{3}}\right)}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$${d}\:={lim}_{{t}\rightarrow−\sqrt{\mathrm{3}}} \:\:\:\left({t}+\sqrt{\mathrm{3}}\right){F}\left({t}\right)\:=\frac{\mathrm{4}}{\mathrm{2}\left(−\mathrm{2}\sqrt{\mathrm{3}}\right)}\:=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\Rightarrow \\ $$$${F}\left({t}\right)\:=−\frac{\mathrm{1}}{\mathrm{2}\left({t}−\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{2}\left({t}+\mathrm{1}\right)}\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}\left({t}−\sqrt{\mathrm{3}}\right)}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}\left({t}+\sqrt{\mathrm{3}}\right)}\:\Rightarrow \\ $$$${I}\:=\mathrm{2}\:\int\:{F}\left({t}\right){dt}\:=−\int\:\frac{{dt}}{{t}−\mathrm{1}}\:+\int\:\frac{{dt}}{{t}+\mathrm{1}}\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\int\:\frac{{dt}}{{t}−\sqrt{\mathrm{3}}}\:−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\int\:\:\frac{{dt}}{{t}+\sqrt{\mathrm{3}}} \\ $$$$={ln}\mid\frac{{t}+\mathrm{1}}{{t}−\mathrm{1}}\mid+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{ln}\mid\frac{{t}−\sqrt{\mathrm{3}}}{{t}+\sqrt{\mathrm{3}}}\mid\:+{C} \\ $$$$={ln}\mid\frac{{tan}\left(\frac{{x}}{\mathrm{2}}\right)+\mathrm{1}}{{tan}\left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{1}}\mid\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{ln}\mid\frac{{tan}\left(\frac{{x}}{\mathrm{2}}\right)−\sqrt{\mathrm{3}}}{{tan}\left(\frac{{x}}{\mathrm{2}}\right)+\sqrt{\mathrm{3}}}\mid\:+{C}\: \\ $$
Answered by Tanmay chaudhury last updated on 22/Jul/19
∫(dx/(cosx+2cos^2 x)) ∫((1+2cosx−2cosx)/(cosx(1+2cosx)))dx ∫secxdx−2∫(dx/(1+((2(1−tan^2 (x/2)))/(1+tan^2 (x/2))))) ∫secxdx−2∫((sec^2 (x/2))/(3−tan^2 (x/2)))dx t=tan(x/2)→dt=sec^2 (x/2)×(1/2)×dx ∫secx−2∫((2dt)/(((√3) )^2 −t^2 )) ∫secx+(2/( (√3)))∫(((t+(√3) )−(t−(√3) ))/((t+(√3) )(t−(√3) )))dt ∫secx dx+(2/( (√3)))∫(dt/(t−(√3)))−(2/( (√3)))∫(dt/(t+(√3))) ln(secx+tanx)+(2/( (√3)))ln(((t−(√3))/(t+(√3))))+c ln(secx+tanx)+(2/( (√3)))ln(((tan(x/2)−(√3))/(tan(x/2)+(√3))))+c
$$\int\frac{{dx}}{{cosx}+\mathrm{2}{cos}^{\mathrm{2}} {x}} \\ $$$$\int\frac{\mathrm{1}+\mathrm{2}{cosx}−\mathrm{2}{cosx}}{{cosx}\left(\mathrm{1}+\mathrm{2}{cosx}\right)}{dx} \\ $$$$\int{secxdx}−\mathrm{2}\int\frac{{dx}}{\mathrm{1}+\frac{\mathrm{2}\left(\mathrm{1}−{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\right)}{\mathrm{1}+{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}} \\ $$$$\int{secxdx}−\mathrm{2}\int\frac{{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{3}−{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{dx} \\ $$$${t}={tan}\frac{{x}}{\mathrm{2}}\rightarrow{dt}={sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}×{dx} \\ $$$$\int{secx}−\mathrm{2}\int\frac{\mathrm{2}{dt}}{\left(\sqrt{\mathrm{3}}\:\right)^{\mathrm{2}} −{t}^{\mathrm{2}} } \\ $$$$\int{secx}+\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\int\frac{\left({t}+\sqrt{\mathrm{3}}\:\right)−\left({t}−\sqrt{\mathrm{3}}\:\right)}{\left({t}+\sqrt{\mathrm{3}}\:\right)\left({t}−\sqrt{\mathrm{3}}\:\right)}{dt} \\ $$$$\int{secx}\:{dx}+\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\int\frac{{dt}}{{t}−\sqrt{\mathrm{3}}}−\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\int\frac{{dt}}{{t}+\sqrt{\mathrm{3}}} \\ $$$${ln}\left({secx}+{tanx}\right)+\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{ln}\left(\frac{{t}−\sqrt{\mathrm{3}}}{{t}+\sqrt{\mathrm{3}}}\right)+{c} \\ $$$${ln}\left({secx}+{tanx}\right)+\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{ln}\left(\frac{{tan}\frac{{x}}{\mathrm{2}}−\sqrt{\mathrm{3}}}{{tan}\frac{{x}}{\mathrm{2}}+\sqrt{\mathrm{3}}}\right)+{c} \\ $$
Commented by Mikael last updated on 22/Jul/19
welcome back Tanmay Sir.
$${welcome}\:{back}\:{Tanmay}\:{Sir}. \\ $$
Answered by MJS last updated on 22/Jul/19
∫(dx/(1+cos x +cos 2x))= [t=tan (x/2) → dx=((2dt)/(t^2 +1))] =2∫((t^2 +1)/((t−(√3))(t−1)(t+1)(t+(√3))))dt= =((2(√3))/3)∫(dt/(t−(√3)))−∫(dt/(t−1))+∫(dt/(t+1))−((2(√3))/3)∫(dt/(t+(√3)))= =ln ∣((t+1)/(t−1))∣ +((2(√3))/3)ln ∣((t−(√3))/(t+(√3)))∣ ...
$$\int\frac{{dx}}{\mathrm{1}+\mathrm{cos}\:{x}\:+\mathrm{cos}\:\mathrm{2}{x}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\rightarrow\:{dx}=\frac{\mathrm{2}{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=\mathrm{2}\int\frac{{t}^{\mathrm{2}} +\mathrm{1}}{\left({t}−\sqrt{\mathrm{3}}\right)\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)\left({t}+\sqrt{\mathrm{3}}\right)}{dt}= \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\int\frac{{dt}}{{t}−\sqrt{\mathrm{3}}}−\int\frac{{dt}}{{t}−\mathrm{1}}+\int\frac{{dt}}{{t}+\mathrm{1}}−\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\int\frac{{dt}}{{t}+\sqrt{\mathrm{3}}}= \\ $$$$=\mathrm{ln}\:\mid\frac{{t}+\mathrm{1}}{{t}−\mathrm{1}}\mid\:+\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{ln}\:\mid\frac{{t}−\sqrt{\mathrm{3}}}{{t}+\sqrt{\mathrm{3}}}\mid \\ $$$$… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *