Question Number 28997 by abdo imad last updated on 03/Feb/18
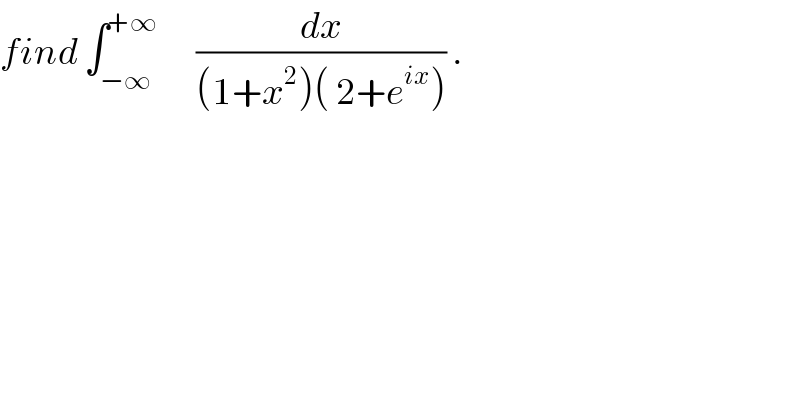
$${find}\:\int_{−\infty} ^{+\infty} \:\:\:\:\:\:\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\:\mathrm{2}+{e}^{{ix}} \right)}\:. \\ $$
Commented by abdo imad last updated on 04/Feb/18

$${let}\:{put}\:{I}=\:\int_{−\infty} ^{+\infty} \:\:\:\:\:\:\:\:\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{2}+{e}^{{ix}} \right)} \\ $$$${I}=\:\:\int_{−\infty} ^{+\infty} \:\:\:\:\:\:\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{2}+{cosx}\:+{isinx}\right)} \\ $$$${I}=\:\int_{−\infty} ^{+\infty} \:\:\frac{\mathrm{2}+{cosx}\:−{isinx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\left(\mathrm{2}+{cosx}\right)^{\mathrm{2}} \:+{sin}^{\mathrm{2}} {x}\right)} \\ $$$${I}\:=\:\int_{−\infty} ^{+\infty} \:\:\:\:\frac{\mathrm{2}+{cosx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{5}\:+\mathrm{4}{cosx}\right)}{dx}\:\:−{i}\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{sinx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{5}+\mathrm{4}{cosx}\right)}{dx} \\ $$$$=\int_{−\infty} ^{+\infty} \:\:\:\:\:\:\frac{\mathrm{2}\:+{cosx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{5}+\mathrm{4}{cosx}\right)}{dx}\:−\mathrm{0}\:{for}\:{another}\:{side} \\ $$$${let}\:{introduce}\:{the}\:{complex}\:{function} \\ $$$${w}\left({z}\right)=\:\:\:\frac{\mathrm{1}}{\left(\mathrm{1}+{z}^{\mathrm{2}} \right)\left(\mathrm{2}\:+{e}^{{iz}} \right)}\:{the}\:{poles}\:{of}\:{w}\:{are}\:{i}\:{and}\:−{i}\left({simple}\right) \\ $$$${by}\:{residus}\:{theorem} \\ $$$$\int_{−\infty} ^{+\infty} \:{w}\left({z}\right){dz}=\mathrm{2}{i}\pi\:{Res}\left({w},{i}\right)\:\:{but} \\ $$$${Res}\left({w},{i}\right)={lim}_{{z}\rightarrow{i}} \left({z}−{i}\right){w}\left({z}\right)=\:{lim}_{{z}\rightarrow{i}} \:\frac{\mathrm{1}}{\left({z}+{i}\right)\left(\mathrm{2}\:+{e}^{{iz}} \right)} \\ $$$$=\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}{i}\left(\:\mathrm{2}\:+\:{e}^{−\mathrm{1}} \right)}\:\Rightarrow\:\int_{−\infty} ^{+\infty} {w}\left({z}\right){dz}=\mathrm{2}{i}\pi\:.\frac{\mathrm{1}}{\mathrm{2}{i}\left(\mathrm{2}+\:{e}^{−\mathrm{1}} \right)} \\ $$$$=\:\:\frac{\pi}{\mathrm{2}\:+\frac{\mathrm{1}}{{e}}}=\:\:\frac{\pi{e}}{\mathrm{2}{e}+\mathrm{1}}\:\Rightarrow \\ $$$${I}=\:\:\frac{\pi{e}}{\mathrm{2}{e}+\mathrm{1}}=\:\int_{−\infty} ^{+\infty} \:\:\:\:\:\:\:\:\frac{\mathrm{2}+{cosx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{5}+\mathrm{4}{cosx}+\right.}{dx}. \\ $$$$ \\ $$
