Question Number 34225 by abdo imad last updated on 03/May/18
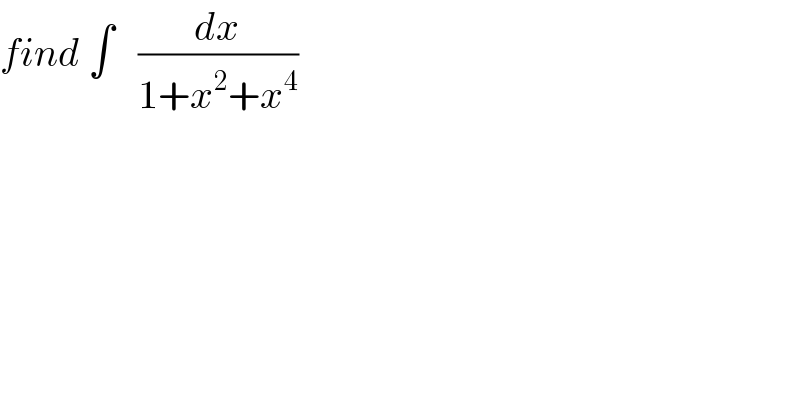
$${find}\:\int\:\:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} } \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 03/May/18

$$\int\frac{\mathrm{1}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}\:} +\mathrm{1}}{dx} \\ $$$$\int\frac{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} \:}+\mathrm{1}} \\ $$$${I}.=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} \:}\right)−\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:\right)}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} \:}+\mathrm{1}}{dx} \\ $$$${I}_{\mathrm{1}=} \frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} \:}\right)}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{3}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}_{\mathrm{1}} }{{t}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{3}}\:{use}\:{formula} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}\:}.{tan}^{−\mathrm{1}} \left(\frac{{t}_{\mathrm{1}} }{\:\sqrt{\mathrm{3}}}\right) \\ $$$${I}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}\:} }\right)}{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{1}} \\ $$$${I}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}.\int\frac{{dt}_{\mathrm{2}} }{{t}_{\mathrm{2}} ^{\mathrm{2}} −\mathrm{1}}\:{use}\:{formula} \\ $$$${I}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{2}}.{ln}\mid\frac{\mathrm{1}−{t}_{\mathrm{2}} }{\mathrm{1}+{t}_{\mathrm{2}} }\mid \\ $$$${I}={I}_{\mathrm{1}} −{I}_{\mathrm{2}} \\ $$
