Question Number 38105 by maxmathsup by imad last updated on 21/Jun/18
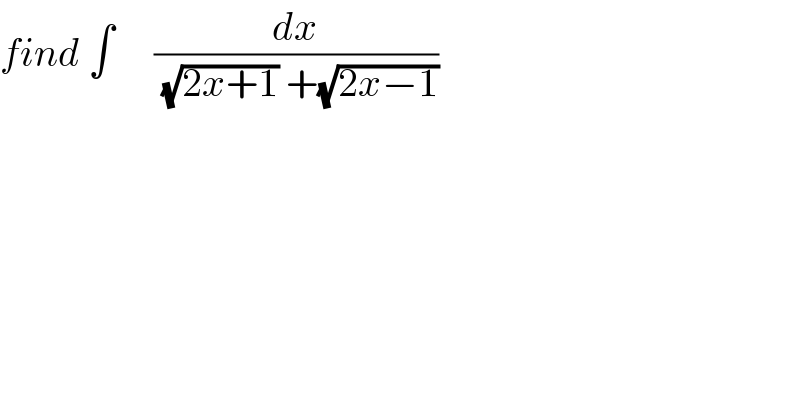
$${find}\:\int\:\:\:\:\:\frac{{dx}}{\:\sqrt{\mathrm{2}{x}+\mathrm{1}}\:+\sqrt{\mathrm{2}{x}−\mathrm{1}}}\: \\ $$
Answered by MJS last updated on 22/Jun/18
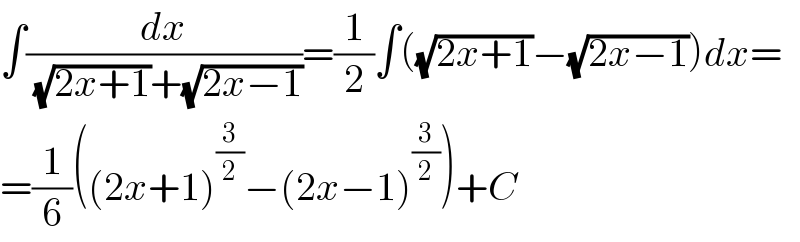
$$\int\frac{{dx}}{\:\sqrt{\mathrm{2}{x}+\mathrm{1}}+\sqrt{\mathrm{2}{x}−\mathrm{1}}}=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\sqrt{\mathrm{2}{x}+\mathrm{1}}−\sqrt{\mathrm{2}{x}−\mathrm{1}}\right){dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left(\left(\mathrm{2}{x}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\left(\mathrm{2}{x}−\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right)+{C} \\ $$
