Question Number 33329 by prof Abdo imad last updated on 14/Apr/18
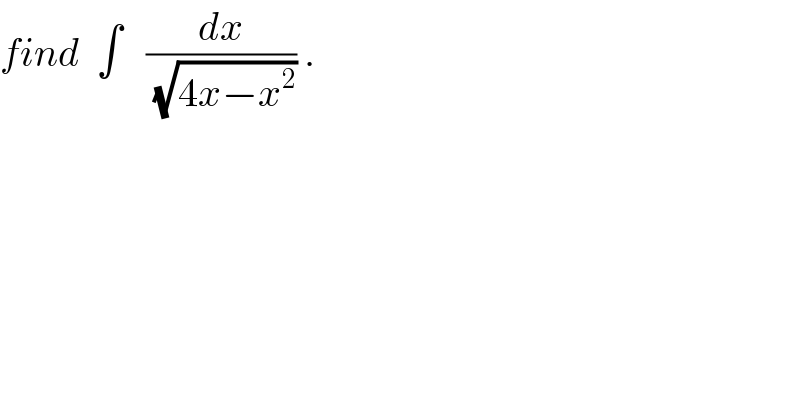
$${find}\:\:\int\:\:\:\frac{{dx}}{\:\sqrt{\mathrm{4}{x}−{x}^{\mathrm{2}} }}\:. \\ $$
Commented by prof Abdo imad last updated on 19/Apr/18
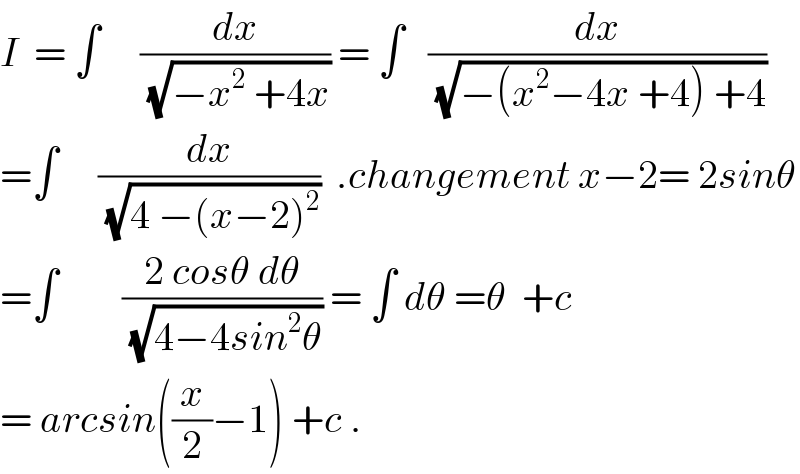
$${I}\:\:=\:\int\:\:\:\:\:\frac{{dx}}{\:\sqrt{−{x}^{\mathrm{2}} \:+\mathrm{4}{x}}}\:=\:\int\:\:\:\frac{{dx}}{\:\sqrt{−\left({x}^{\mathrm{2}} −\mathrm{4}{x}\:+\mathrm{4}\right)\:+\mathrm{4}}} \\ $$$$=\int\:\:\:\:\:\frac{{dx}}{\:\sqrt{\mathrm{4}\:−\left({x}−\mathrm{2}\right)^{\mathrm{2}} }}\:\:.{changement}\:{x}−\mathrm{2}=\:\mathrm{2}{sin}\theta \\ $$$$=\int\:\:\:\:\:\:\:\:\frac{\mathrm{2}\:{cos}\theta\:{d}\theta}{\:\sqrt{\mathrm{4}−\mathrm{4}{sin}^{\mathrm{2}} \theta}}\:=\:\int\:{d}\theta\:=\theta\:\:+{c} \\ $$$$=\:{arcsin}\left(\frac{{x}}{\mathrm{2}}−\mathrm{1}\right)\:+{c}\:. \\ $$
