Menu Close

find-dx-cos-4-x-sin-4-x-

Tinku Tara 0 Comments
Pin




Question Number 36428 by prof Abdo imad last updated on 02/Jun/18
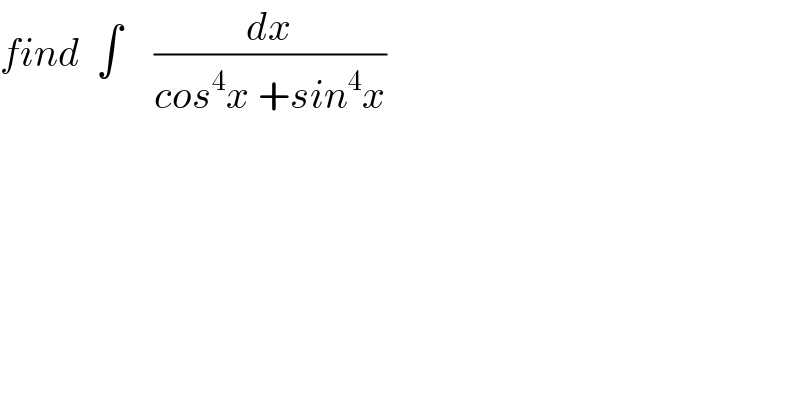
find ∫ (dx/(cos^4 x +sin^4 x))
$${find}\:\:\int\:\:\:\:\frac{{dx}}{{cos}^{\mathrm{4}} {x}\:+{sin}^{\mathrm{4}} {x}} \\ $$
Commented by abdo.msup.com last updated on 02/Jun/18
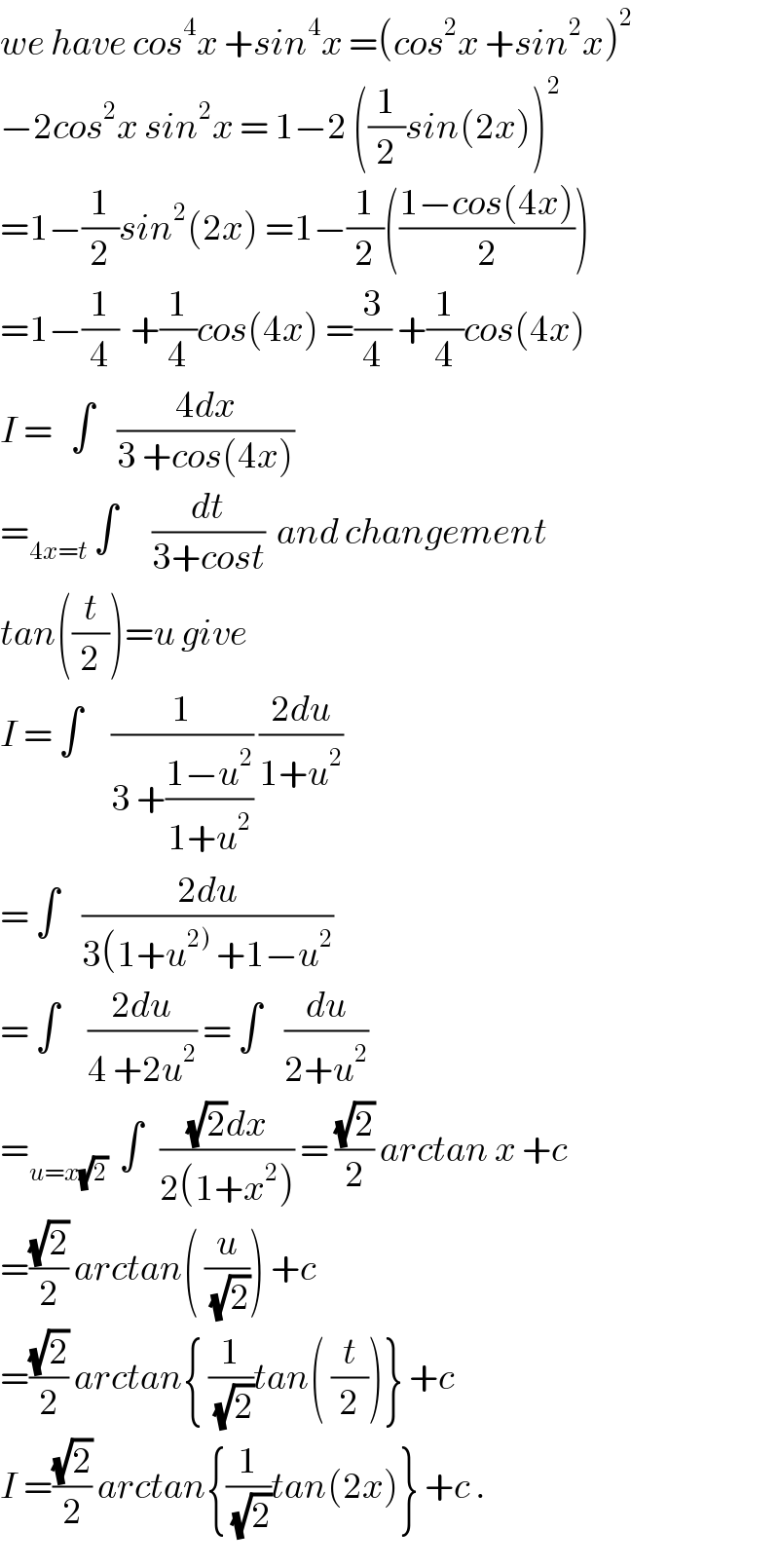
we have cos^4 x +sin^4 x =(cos^2 x +sin^2 x)^2 −2cos^2 x sin^2 x = 1−2 ((1/2)sin(2x))^2 =1−(1/2)sin^2 (2x) =1−(1/2)(((1−cos(4x))/2)) =1−(1/4) +(1/4)cos(4x) =(3/4) +(1/4)cos(4x) I = ∫ ((4dx)/(3 +cos(4x))) =_(4x=t) ∫ (dt/(3+cost)) and changement tan((t/2))=u give I = ∫ (1/(3 +((1−u^2 )/(1+u^2 )))) ((2du)/(1+u^2 )) = ∫ ((2du)/(3(1+u^(2)) +1−u^2 )) = ∫ ((2du)/(4 +2u^2 )) = ∫ (du/(2+u^2 )) =_(u=x(√2)) ∫ (((√2)dx)/(2(1+x^2 ))) = ((√2)/2) arctan x +c =((√2)/2) arctan( (u/( (√2)))) +c =((√2)/2) arctan{ (1/( (√2)))tan( (t/2))} +c I =((√2)/2) arctan{(1/( (√2)))tan(2x)} +c .
$${we}\:{have}\:{cos}^{\mathrm{4}} {x}\:+{sin}^{\mathrm{4}} {x}\:=\left({cos}^{\mathrm{2}} {x}\:+{sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} \\ $$$$−\mathrm{2}{cos}^{\mathrm{2}} {x}\:{sin}^{\mathrm{2}} {x}\:=\:\mathrm{1}−\mathrm{2}\:\left(\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}{x}\right)\right)^{\mathrm{2}} \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{sin}^{\mathrm{2}} \left(\mathrm{2}{x}\right)\:=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}−{cos}\left(\mathrm{4}{x}\right)}{\mathrm{2}}\right) \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\:\:+\frac{\mathrm{1}}{\mathrm{4}}{cos}\left(\mathrm{4}{x}\right)\:=\frac{\mathrm{3}}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{4}}{cos}\left(\mathrm{4}{x}\right) \\ $$$${I}\:=\:\:\:\int\:\:\:\:\frac{\mathrm{4}{dx}}{\mathrm{3}\:+{cos}\left(\mathrm{4}{x}\right)} \\ $$$$=_{\mathrm{4}{x}={t}} \:\int\:\:\:\:\:\:\frac{{dt}}{\mathrm{3}+{cost}}\:\:{and}\:{changement} \\ $$$${tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}\:{give} \\ $$$${I}\:=\:\int\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{3}\:+\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }}\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\:\int\:\:\:\:\frac{\mathrm{2}{du}}{\mathrm{3}\left(\mathrm{1}+{u}^{\left.\mathrm{2}\right)} \:+\mathrm{1}−{u}^{\mathrm{2}} \right.} \\ $$$$=\:\int\:\:\:\:\:\frac{\mathrm{2}{du}}{\mathrm{4}\:+\mathrm{2}{u}^{\mathrm{2}} }\:=\:\int\:\:\:\:\frac{{du}}{\mathrm{2}+{u}^{\mathrm{2}} } \\ $$$$=_{{u}={x}\sqrt{\mathrm{2}}} \:\:\int\:\:\:\frac{\sqrt{\mathrm{2}}{dx}}{\mathrm{2}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:{arctan}\:{x}\:+{c} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:{arctan}\left(\:\frac{{u}}{\:\sqrt{\mathrm{2}}}\right)\:+{c} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:{arctan}\left\{\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{tan}\left(\:\frac{{t}}{\mathrm{2}}\right)\right\}\:+{c} \\ $$$${I}\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:{arctan}\left\{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{tan}\left(\mathrm{2}{x}\right)\right\}\:+{c}\:. \\ $$
Answered by MJS last updated on 02/Jun/18
∫(dx/(cos^4 x +sin^4 x))= [sin x=((tan x)/(sec x)); cos x=(1/(sec x)); sec^2 x=1+tan^2 x] =∫sec^2 x((1+tan^2 x)/(1+tan^4 x))dx= [t=tan x → dx=(dt/(sec^2 x))] =∫((t^2 +1)/(t^4 +1))dt=∫((t^2 +1)/((t^2 −(√2)t+1)(t^2 +(√2)t+1)))dt= =(1/2)(∫(dt/(t^2 −(√2)t+1))+∫(dt/(t^2 +(√2)t+1)))= [((∫(dt/(t^2 ±pt+q))=∫(dt/((t±(p/2))^2 +q−(p^2 /4)))=)),(( [u=((2t±p)/(2(√(q−(p^2 /4))))) → dt=(√(q−(p^2 /4)))du])),((=(2/( (√(4q−p^2 ))))∫(du/(u^2 +1))=(2/( (√(4q−p^2 ))))arctan u=)),((=(2/( (√(4q−p^2 ))))arctan(((2t±p)/( (√(4q−p^2 ))))))) ] =((√2)/2)(arctan((√2)tan x −1)+arctan((√2)tan x +1))+C
$$\int\frac{{dx}}{\mathrm{cos}^{\mathrm{4}} \:{x}\:+\mathrm{sin}^{\mathrm{4}} \:{x}}= \\ $$$$\:\:\:\:\:\left[\mathrm{sin}\:{x}=\frac{\mathrm{tan}\:{x}}{\mathrm{sec}\:{x}};\:\mathrm{cos}\:{x}=\frac{\mathrm{1}}{\mathrm{sec}\:{x}};\:\mathrm{sec}^{\mathrm{2}} \:{x}=\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:{x}\right] \\ $$$$=\int\mathrm{sec}^{\mathrm{2}} \:{x}\frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:{x}}{\mathrm{1}+\mathrm{tan}^{\mathrm{4}} \:{x}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{sec}^{\mathrm{2}} \:{x}}\right] \\ $$$$=\int\frac{{t}^{\mathrm{2}} +\mathrm{1}}{{t}^{\mathrm{4}} +\mathrm{1}}{dt}=\int\frac{{t}^{\mathrm{2}} +\mathrm{1}}{\left({t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{1}\right)}{dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\int\frac{{dt}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{1}}+\int\frac{{dt}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{1}}\right)= \\ $$$$ \\ $$$$\:\:\:\:\:\begin{bmatrix}{\int\frac{{dt}}{{t}^{\mathrm{2}} \pm{pt}+{q}}=\int\frac{{dt}}{\left({t}\pm\frac{{p}}{\mathrm{2}}\right)^{\mathrm{2}} +{q}−\frac{{p}^{\mathrm{2}} }{\mathrm{4}}}=}\\{\:\:\:\:\:\left[{u}=\frac{\mathrm{2}{t}\pm{p}}{\mathrm{2}\sqrt{{q}−\frac{{p}^{\mathrm{2}} }{\mathrm{4}}}}\:\rightarrow\:{dt}=\sqrt{{q}−\frac{{p}^{\mathrm{2}} }{\mathrm{4}}}{du}\right]}\\{=\frac{\mathrm{2}}{\:\sqrt{\mathrm{4}{q}−{p}^{\mathrm{2}} }}\int\frac{{du}}{{u}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{4}{q}−{p}^{\mathrm{2}} }}\mathrm{arctan}\:{u}=}\\{=\frac{\mathrm{2}}{\:\sqrt{\mathrm{4}{q}−{p}^{\mathrm{2}} }}\mathrm{arctan}\left(\frac{\mathrm{2}{t}\pm{p}}{\:\sqrt{\mathrm{4}{q}−{p}^{\mathrm{2}} }}\right)}\end{bmatrix} \\ $$$$ \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{arctan}\left(\sqrt{\mathrm{2}}\mathrm{tan}\:{x}\:−\mathrm{1}\right)+\mathrm{arctan}\left(\sqrt{\mathrm{2}}\mathrm{tan}\:{x}\:+\mathrm{1}\right)\right)+{C} \\ $$
Answered by MJS last updated on 02/Jun/18
better: ∫(dx/(cos^4 x +sin^4 x))=4∫(dx/(cos 4x +3))= [t=4x → dx=(dt/4)] =∫(dt/(cos t +3))=∫((sec^2 (t/2))/(2(tan^2 (t/2)+2)))dt= [u=((√2)/2)tan (t/2) → dt=((2(√2))/(sec^2 (t/2)))du] =((√2)/2)∫(du/(u^2 +1))=((√2)/2)arctan u=((√2)/2)arctan(((√2)/2)tan (t/2))= =((√2)/2)arctan(((√2)/2)tan 2x)+C
$$\mathrm{better}: \\ $$$$\int\frac{{dx}}{\mathrm{cos}^{\mathrm{4}} \:{x}\:+\mathrm{sin}^{\mathrm{4}} \:{x}}=\mathrm{4}\int\frac{{dx}}{\mathrm{cos}\:\mathrm{4}{x}\:+\mathrm{3}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{4}{x}\:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{4}}\right] \\ $$$$=\int\frac{{dt}}{\mathrm{cos}\:{t}\:+\mathrm{3}}=\int\frac{\mathrm{sec}^{\mathrm{2}} \:\frac{{t}}{\mathrm{2}}}{\mathrm{2}\left(\mathrm{tan}^{\mathrm{2}} \:\frac{{t}}{\mathrm{2}}+\mathrm{2}\right)}{dt}= \\ $$$$\:\:\:\:\:\left[{u}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{tan}\:\frac{{t}}{\mathrm{2}}\:\rightarrow\:{dt}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{sec}^{\mathrm{2}} \:\frac{{t}}{\mathrm{2}}}{du}\right] \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\int\frac{{du}}{{u}^{\mathrm{2}} +\mathrm{1}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{arctan}\:{u}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{arctan}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{tan}\:\frac{{t}}{\mathrm{2}}\right)= \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{arctan}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{tan}\:\mathrm{2}{x}\right)+{C} \\ $$
Commented by abdo.msup.com last updated on 02/Jun/18
thank you sir Mjs you are really talented in maths..
$${thank}\:{you}\:{sir}\:{Mjs}\:\:{you}\:{are}\:{really} \\ $$$${talented}\:{in}\:{maths}.. \\ $$
Commented by rahul 19 last updated on 03/Jun/18
Nice !
$$\mathrm{Nice}\:! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *