find-dx-sinx-sin-2x-

Question Number 29445 by prof Abdo imad last updated on 08/Feb/18

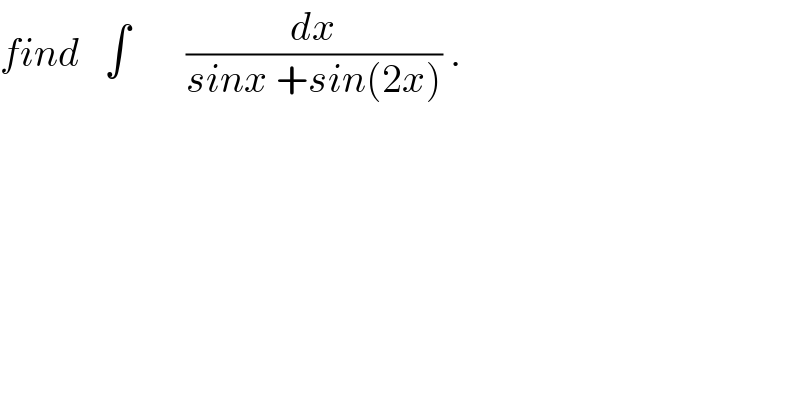
f i n d \int \frac{d x}{s i n x + s i n (2 x)} .

Answered by mrW2 last updated on 09/Feb/18

= \int \frac{d x}{\sin x (1 + 2 \cos x)}

= \int \frac{\sin x d x}{\sin^{2} x (1 + 2 \cos x)}

= \int \frac{d (\cos x)}{(\cos^{2} x - 1) (2 \cos x + 1)}

= \int \frac{d t}{(t^{2} - 1) (2 t + 1)}

= \int [- \frac{1}{2 (t + 1)} - \frac{1}{6 (t - 1)} + \frac{4}{3 (2 t + 1)}] d t

= - \frac{\ln (t + 1)}{2} - \frac{\ln (t - 1)}{6} + \frac{2 \ln (2 t + 1)}{3} + C

= - \frac{3 \ln (t + 1)}{6} - \frac{\ln (t - 1)}{6} + \frac{4 \ln (2 t + 1)}{6} + C

= - \frac{\ln {(t + 1)}^{3}}{6} - \frac{\ln (t - 1)}{6} + \frac{\ln {(2 t + 1)}^{4}}{6} + C

= \frac{1}{6} \ln ∣ \frac{{(2 t + 1)}^{4}}{{(t + 1)}^{3} (t - 1)} ∣ + C

= \frac{1}{6} \ln ∣ \frac{{(2 \cos x + 1)}^{4}}{{(\cos x + 1)}^{3} (\cos x - 1)} ∣ + C

= \frac{1}{6} \ln ∣ \frac{{(2 \cos x + 1)}^{4}}{{(\cos x + 1)}^{2} (\sin^{2} x)} ∣ + C

= \frac{1}{3} \ln ∣ \frac{{(2 \cos x + 1)}^{2}}{\sin x (\cos x + 1)} ∣ + C

Facebook Tweet Pin