Menu Close

find-dx-x-1-3-x-2-3-2-

Tinku Tara 0 Comments
Pin




Question Number 81432 by abdomathmax last updated on 13/Feb/20
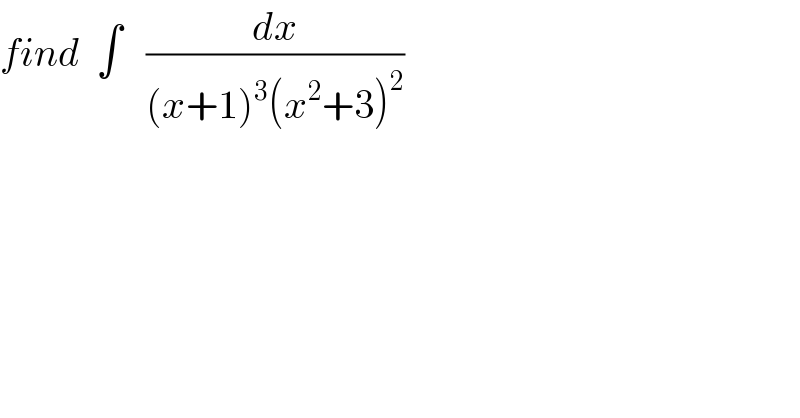
find ∫ (dx/((x+1)^3 (x^2 +3)^2 ))
$${find}\:\:\int\:\:\:\frac{{dx}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} } \\ $$
Commented by abdomathmax last updated on 20/Feb/20
let try complex method I =∫ (dx/((x+1)^3 (x^2 +3)^2 ))dx ⇒I=∫ (dx/((x+1)^3 (x−i(√3))^2 (x+i(√3))^2 )) =∫ (dx/((((x+1)/(x+i(√3))))^3 ×(x+i(√3))^5 (x−i(√3))^2 )) changement ((x+1)/(x+i(√3))) =t give x+1=tx+i(√3)t ⇒ (1−t)x=i(√3)t−1 ⇒x=((i(√3)t−1)/(1−t)) dx =((i(√3)(1−t)−(i(√3)t−1)(−1))/((1−t)^2 ))dt =((i(√3)−i(√3)t+i(√3)t−1)/((t−1)^2 ))dt =((i(√3)−1)/((t−1)^2 ))dt x+i(√3)=((i(√3)t−1)/(1−t)) +i(√3)=((i(√3)t−1+i(√3)−i(√3)t)/(1−t)) =((i(√3)−1)/(1−t)) =((1−i(√3))/(t−1)) x−i(√3)=((i(√3)t−1)/(1−t))−i(√3)=((i(√3)t−1−i(√3)+i(√3)t)/((1−t))) =((2i(√3)t−1−i(√3))/((1−t))) =((−2i(√3)t+1+i(√3))/((t−1))) ⇒ I =(i(√3)−1) ∫ (dt/((t−1)^2 t^3 (((1−i(√3))/(t−1)))^5 (((−2i(√3)t+1+i(√3))/(t−1)))^2 )) =(i(√3)−1) ∫ (((t−1)^7 dt)/((t−1)^2 t^3 (−2i(√3)t +1+i(√3))^2 (1−i(√3))^5 )) =−(1/((i(√3)−1)^4 )) ∫ (((t−1)^5 )/(t^3 (−2i(√3)t +i(√3))^2 ))dt =(1/(3(i(√3)−1)^4 )) ∫ (((t−1)^5 )/(t^2 (−2t+1)^2 ))dt =λ ∫ ((Σ_(k=0) ^5 C_5 ^k t^k (−1)^(5−k) )/(t^2 (2t−1)^2 ))dt (λ=(1/(3(i(√3)−1)^4 ))) =λ∫ ((− C_5 ^0 +C_5 ^1 t−C_5 ^2 t^2 +C_5 ^3 t^3 −C_5 ^4 t^4 +C_5 ^5 t^5 )/(t^2 (2t−1)^2 ))dt =λ ∫ {−(C_5 ^0 /(t^2 (2t−1)^2 ))+(C_5 ^1 /(t(2t−1)^2 ))−(C_5 ^2 /((2t−1)^2 )) +((C_5 ^3 t)/((2t−1)^2 )) −((C_5 ^4 t^2 )/((2t−1)^2 )) +((C_5 ^5 t^5 )/((2t−1)^2 ))}dt ...be continued...
$${let}\:{try}\:{complex}\:{method}\:{I}\:=\int\:\:\frac{{dx}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }{dx}\:\Rightarrow{I}=\int\:\:\frac{{dx}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}−{i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \left({x}+{i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$$=\int\:\:\:\frac{{dx}}{\left(\frac{{x}+\mathrm{1}}{{x}+{i}\sqrt{\mathrm{3}}}\right)^{\mathrm{3}} ×\left({x}+{i}\sqrt{\mathrm{3}}\right)^{\mathrm{5}} \left({x}−{i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$${changement}\:\frac{{x}+\mathrm{1}}{{x}+{i}\sqrt{\mathrm{3}}}\:={t}\:{give}\:{x}+\mathrm{1}={tx}+{i}\sqrt{\mathrm{3}}{t}\:\Rightarrow \\ $$$$\left(\mathrm{1}−{t}\right){x}={i}\sqrt{\mathrm{3}}{t}−\mathrm{1}\:\Rightarrow{x}=\frac{{i}\sqrt{\mathrm{3}}{t}−\mathrm{1}}{\mathrm{1}−{t}} \\ $$$${dx}\:=\frac{{i}\sqrt{\mathrm{3}}\left(\mathrm{1}−{t}\right)−\left({i}\sqrt{\mathrm{3}}{t}−\mathrm{1}\right)\left(−\mathrm{1}\right)}{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} }{dt} \\ $$$$=\frac{{i}\sqrt{\mathrm{3}}−{i}\sqrt{\mathrm{3}}{t}+{i}\sqrt{\mathrm{3}}{t}−\mathrm{1}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }{dt}\:=\frac{{i}\sqrt{\mathrm{3}}−\mathrm{1}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }{dt} \\ $$$${x}+{i}\sqrt{\mathrm{3}}=\frac{{i}\sqrt{\mathrm{3}}{t}−\mathrm{1}}{\mathrm{1}−{t}}\:+{i}\sqrt{\mathrm{3}}=\frac{{i}\sqrt{\mathrm{3}}{t}−\mathrm{1}+{i}\sqrt{\mathrm{3}}−{i}\sqrt{\mathrm{3}}{t}}{\mathrm{1}−{t}} \\ $$$$=\frac{{i}\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{1}−{t}}\:=\frac{\mathrm{1}−{i}\sqrt{\mathrm{3}}}{{t}−\mathrm{1}} \\ $$$${x}−{i}\sqrt{\mathrm{3}}=\frac{{i}\sqrt{\mathrm{3}}{t}−\mathrm{1}}{\mathrm{1}−{t}}−{i}\sqrt{\mathrm{3}}=\frac{{i}\sqrt{\mathrm{3}}{t}−\mathrm{1}−{i}\sqrt{\mathrm{3}}+{i}\sqrt{\mathrm{3}}{t}}{\left(\mathrm{1}−{t}\right)} \\ $$$$=\frac{\mathrm{2}{i}\sqrt{\mathrm{3}}{t}−\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\left(\mathrm{1}−{t}\right)}\:=\frac{−\mathrm{2}{i}\sqrt{\mathrm{3}}{t}+\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\left({t}−\mathrm{1}\right)}\:\Rightarrow \\ $$$${I}\:=\left({i}\sqrt{\mathrm{3}}−\mathrm{1}\right)\:\int\:\:\:\:\frac{{dt}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} \:{t}^{\mathrm{3}} \left(\frac{\mathrm{1}−{i}\sqrt{\mathrm{3}}}{{t}−\mathrm{1}}\right)^{\mathrm{5}} \left(\frac{−\mathrm{2}{i}\sqrt{\mathrm{3}}{t}+\mathrm{1}+{i}\sqrt{\mathrm{3}}}{{t}−\mathrm{1}}\right)^{\mathrm{2}} } \\ $$$$=\left({i}\sqrt{\mathrm{3}}−\mathrm{1}\right)\:\int\:\:\frac{\left({t}−\mathrm{1}\right)^{\mathrm{7}} \:{dt}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} {t}^{\mathrm{3}} \left(−\mathrm{2}{i}\sqrt{\mathrm{3}}{t}\:+\mathrm{1}+{i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \left(\mathrm{1}−{i}\sqrt{\mathrm{3}}\right)^{\mathrm{5}} } \\ $$$$=−\frac{\mathrm{1}}{\left({i}\sqrt{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{4}} }\:\int\:\:\:\frac{\left({t}−\mathrm{1}\right)^{\mathrm{5}} }{{t}^{\mathrm{3}} \left(−\mathrm{2}{i}\sqrt{\mathrm{3}}{t}\:+{i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}\left({i}\sqrt{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{4}} }\:\int\:\:\:\frac{\left({t}−\mathrm{1}\right)^{\mathrm{5}} }{{t}^{\mathrm{2}} \left(−\mathrm{2}{t}+\mathrm{1}\right)^{\mathrm{2}} }{dt} \\ $$$$=\lambda\:\int\:\:\frac{\sum_{{k}=\mathrm{0}} ^{\mathrm{5}} \:{C}_{\mathrm{5}} ^{{k}} \:{t}^{{k}} \left(−\mathrm{1}\right)^{\mathrm{5}−{k}} }{{t}^{\mathrm{2}} \left(\mathrm{2}{t}−\mathrm{1}\right)^{\mathrm{2}} }{dt}\:\:\:\:\left(\lambda=\frac{\mathrm{1}}{\mathrm{3}\left({i}\sqrt{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{4}} }\right) \\ $$$$=\lambda\int\:\:\frac{−\:{C}_{\mathrm{5}} ^{\mathrm{0}} \:+{C}_{\mathrm{5}} ^{\mathrm{1}} \:{t}−{C}_{\mathrm{5}} ^{\mathrm{2}} \:{t}^{\mathrm{2}} \:+{C}_{\mathrm{5}} ^{\mathrm{3}} \:{t}^{\mathrm{3}} \:−{C}_{\mathrm{5}} ^{\mathrm{4}} \:{t}^{\mathrm{4}} \:+{C}_{\mathrm{5}} ^{\mathrm{5}} \:{t}^{\mathrm{5}} }{{t}^{\mathrm{2}} \left(\mathrm{2}{t}−\mathrm{1}\right)^{\mathrm{2}} }{dt} \\ $$$$=\lambda\:\int\:\left\{−\frac{{C}_{\mathrm{5}} ^{\mathrm{0}} }{{t}^{\mathrm{2}} \left(\mathrm{2}{t}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{{C}_{\mathrm{5}} ^{\mathrm{1}} }{{t}\left(\mathrm{2}{t}−\mathrm{1}\right)^{\mathrm{2}} }−\frac{{C}_{\mathrm{5}} ^{\mathrm{2}} }{\left(\mathrm{2}{t}−\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{{C}_{\mathrm{5}} ^{\mathrm{3}} {t}}{\left(\mathrm{2}{t}−\mathrm{1}\right)^{\mathrm{2}} }\right. \\ $$$$\left.−\frac{{C}_{\mathrm{5}} ^{\mathrm{4}} \:{t}^{\mathrm{2}} }{\left(\mathrm{2}{t}−\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{{C}_{\mathrm{5}} ^{\mathrm{5}} {t}^{\mathrm{5}} }{\left(\mathrm{2}{t}−\mathrm{1}\right)^{\mathrm{2}} }\right\}{dt}\:…{be}\:{continued}… \\ $$
Answered by MJS last updated on 13/Feb/20
∫(dx/((x+1)^3 (x^2 +3)^2 ))= Q_1 (x)=(x+1)^2 (x^2 +3) Q_2 (x)=(x+1)(x^2 +3) P_1 (x)=−(1/(12))x^3 −((13)/(96))x^2 −(5/(24))x−(9/(32)) P_2 (x)=−(x/(12))−(1/(48)) =−((8x^3 +13x^2 +20x+27)/(96(x+1)^2 (x^2 +3)))−(1/(48))∫((4x+1)/((x+1)(x^2 +3)))dx ∫((4x+1)/((x+1)(x^2 +3)))dx=−(3/4)∫(dx/(x+1))+(1/4)∫((3x+13)/(x^2 +3))dx= =−(3/4)ln ∣x+1∣ +(3/8)ln (x^2 +3) +((13(√3))/(12))arctan (((√3)x)/3)= =(3/8)ln ((x^2 +3)/((x+1)^2 )) +((13(√3))/(12))arctan (((√3)x)/3) =−((8x^3 +13x^2 +20x+27)/(96(x+1)^2 (x^2 +3)))−(1/(128))ln ((x^2 +3)/((x+1)^2 )) −((13(√3))/(576))arctan (((√3)x)/3) +C
$$\int\frac{{dx}}{\left({x}+\mathrm{1}\right)^{\mathrm{3}} \left({x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:{Q}_{\mathrm{1}} \left({x}\right)=\left({x}+\mathrm{1}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{3}\right) \\ $$$$\:\:\:\:\:{Q}_{\mathrm{2}} \left({x}\right)=\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{3}\right) \\ $$$$\:\:\:\:\:{P}_{\mathrm{1}} \left({x}\right)=−\frac{\mathrm{1}}{\mathrm{12}}{x}^{\mathrm{3}} −\frac{\mathrm{13}}{\mathrm{96}}{x}^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{24}}{x}−\frac{\mathrm{9}}{\mathrm{32}} \\ $$$$\:\:\:\:\:{P}_{\mathrm{2}} \left({x}\right)=−\frac{{x}}{\mathrm{12}}−\frac{\mathrm{1}}{\mathrm{48}} \\ $$$$=−\frac{\mathrm{8}{x}^{\mathrm{3}} +\mathrm{13}{x}^{\mathrm{2}} +\mathrm{20}{x}+\mathrm{27}}{\mathrm{96}\left({x}+\mathrm{1}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{3}\right)}−\frac{\mathrm{1}}{\mathrm{48}}\int\frac{\mathrm{4}{x}+\mathrm{1}}{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{3}\right)}{dx} \\ $$$$\:\:\:\:\:\int\frac{\mathrm{4}{x}+\mathrm{1}}{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{3}\right)}{dx}=−\frac{\mathrm{3}}{\mathrm{4}}\int\frac{{dx}}{{x}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{3}{x}+\mathrm{13}}{{x}^{\mathrm{2}} +\mathrm{3}}{dx}= \\ $$$$\:\:\:\:\:=−\frac{\mathrm{3}}{\mathrm{4}}\mathrm{ln}\:\mid{x}+\mathrm{1}\mid\:+\frac{\mathrm{3}}{\mathrm{8}}\mathrm{ln}\:\left({x}^{\mathrm{2}} +\mathrm{3}\right)\:+\frac{\mathrm{13}\sqrt{\mathrm{3}}}{\mathrm{12}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}{x}}{\mathrm{3}}= \\ $$$$\:\:\:\:\:=\frac{\mathrm{3}}{\mathrm{8}}\mathrm{ln}\:\frac{{x}^{\mathrm{2}} +\mathrm{3}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{\mathrm{13}\sqrt{\mathrm{3}}}{\mathrm{12}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}{x}}{\mathrm{3}} \\ $$$$=−\frac{\mathrm{8}{x}^{\mathrm{3}} +\mathrm{13}{x}^{\mathrm{2}} +\mathrm{20}{x}+\mathrm{27}}{\mathrm{96}\left({x}+\mathrm{1}\right)^{\mathrm{2}} \left({x}^{\mathrm{2}} +\mathrm{3}\right)}−\frac{\mathrm{1}}{\mathrm{128}}\mathrm{ln}\:\frac{{x}^{\mathrm{2}} +\mathrm{3}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }\:−\frac{\mathrm{13}\sqrt{\mathrm{3}}}{\mathrm{576}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}{x}}{\mathrm{3}}\:+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *