find-dx-x-1-x-2-

Question Number 31516 by abdo imad last updated on 09/Mar/18

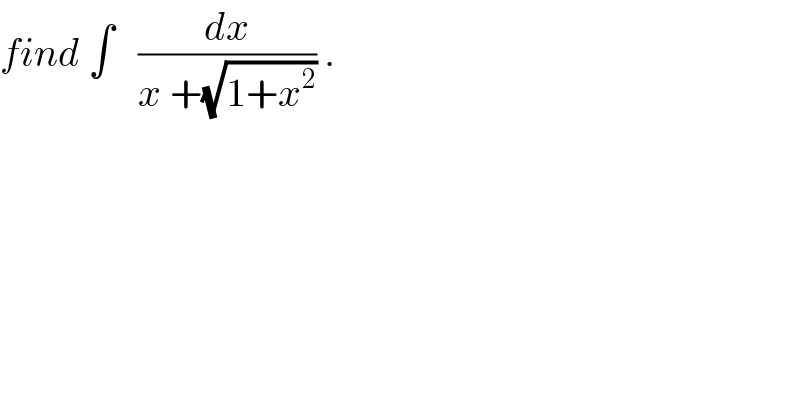
$${find}\:\int\:\:\:\frac{{dx}}{{x}\:+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:. \\ $$

Commented by abdo imad last updated on 16/Mar/18

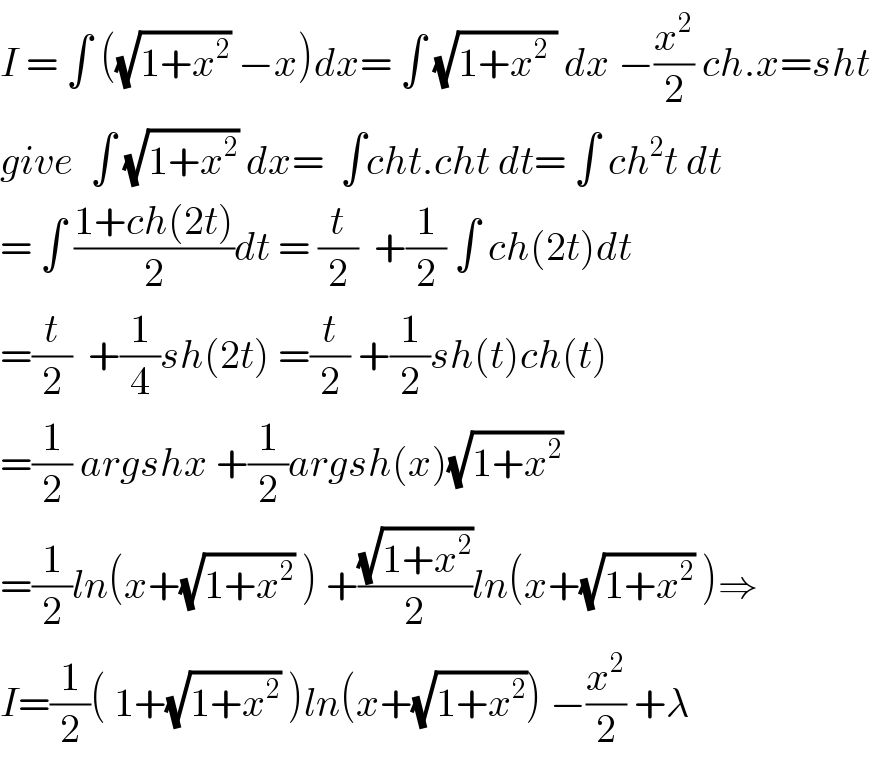
I = ∫ ((√(1+x^2 )) −x)dx= ∫ (√(1+x^2 )) dx −(x^2 /2) ch.x=sht give ∫ (√(1+x^2 )) dx= ∫cht.cht dt= ∫ ch^2 t dt = ∫ ((1+ch(2t))/2)dt = (t/2) +(1/2) ∫ ch(2t)dt =(t/2) +(1/4)sh(2t) =(t/2) +(1/2)sh(t)ch(t) =(1/2) argshx +(1/2)argsh(x)(√(1+x^2 )) =(1/2)ln(x+(√(1+x^2 )) ) +((√(1+x^2 ))/2)ln(x+(√(1+x^2 )) )⇒ I=(1/2)( 1+(√(1+x^2 )) )ln(x+(√(1+x^2 ))) −(x^2 /2) +λ

$${I}\:=\:\int\:\left(\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:−{x}\right){dx}=\:\int\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} \:}\:{dx}\:−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:{ch}.{x}={sht} \\ $$$${give}\:\:\int\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}=\:\:\int{cht}.{cht}\:{dt}=\:\int\:{ch}^{\mathrm{2}} {t}\:{dt} \\ $$$$=\:\int\:\frac{\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)}{\mathrm{2}}{dt}\:=\:\frac{{t}}{\mathrm{2}}\:\:+\frac{\mathrm{1}}{\mathrm{2}}\:\int\:{ch}\left(\mathrm{2}{t}\right){dt} \\ $$$$=\frac{{t}}{\mathrm{2}}\:\:+\frac{\mathrm{1}}{\mathrm{4}}{sh}\left(\mathrm{2}{t}\right)\:=\frac{{t}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}{sh}\left({t}\right){ch}\left({t}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:{argshx}\:+\frac{\mathrm{1}}{\mathrm{2}}{argsh}\left({x}\right)\sqrt{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\right)\:+\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{\mathrm{2}}{ln}\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\right)\Rightarrow \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\left(\:\mathrm{1}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\right){ln}\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)\:−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+\lambda \\ $$

Answered by math1967 last updated on 18/Mar/18

∫((x−(√(1+x^2 )) )/(x^2 −1−x^2 ))dx ∫(√(1+x^2 )) dx −∫xdx ((x(√(1+x^2 )) )/2)+(1/2)log[x+(√(1+x^2 ))] −(x^2 /2) +C

$$\int\frac{{x}−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} \:}\:}{{x}^{\mathrm{2}} −\mathrm{1}−{x}^{\mathrm{2}} }{dx} \\ $$$$\int\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:−\int{xdx} \\ $$$$\frac{{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{log}\left[{x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} \:}\right]\:−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+{C} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply