Question Number 42791 by maxmathsup by imad last updated on 02/Sep/18
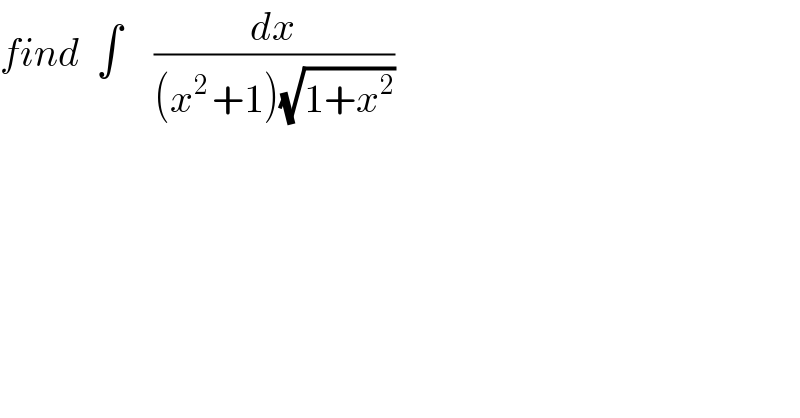
$${find}\:\:\int\:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}\:} +\mathrm{1}\right)\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$
Answered by MJS last updated on 02/Sep/18

$$\mathrm{I}\:\mathrm{know}\:\mathrm{this}\:\mathrm{because}\:\mathrm{of}\:\mathrm{the}\:\mathrm{hyperbola}\:\mathrm{formuls} \\ $$$${y}=\sqrt{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$${y}'=\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${y}''=\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$\Rightarrow\:\int\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}=\int\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }=\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}+{C} \\ $$
Commented by math khazana by abdo last updated on 03/Sep/18

$${thank}\:{you}\:{sir}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Sep/18
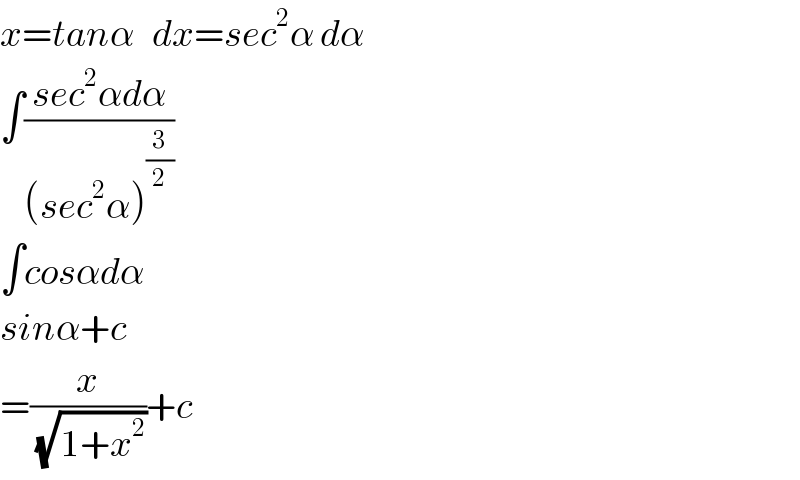
$${x}={tan}\alpha\:\:\:{dx}={sec}^{\mathrm{2}} \alpha\:{d}\alpha \\ $$$$\int\frac{{sec}^{\mathrm{2}} \alpha{d}\alpha}{\left({sec}^{\mathrm{2}} \alpha\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$\int{cos}\alpha{d}\alpha \\ $$$${sin}\alpha+{c} \\ $$$$=\frac{{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}+{c} \\ $$
