Question Number 93873 by mathmax by abdo last updated on 15/May/20
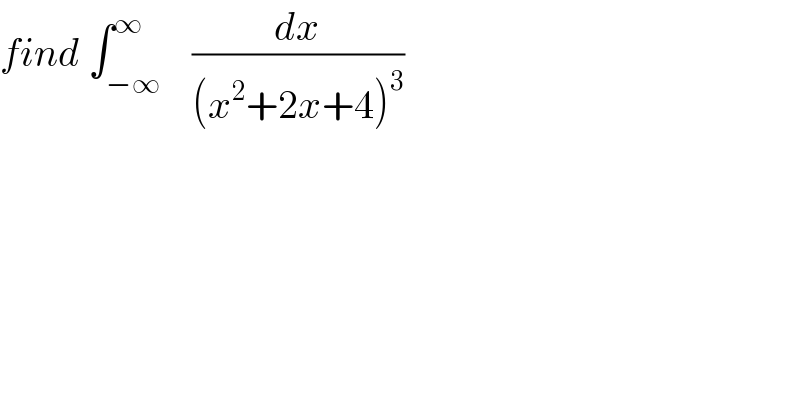
$${find}\:\int_{−\infty} ^{\infty} \:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}\right)^{\mathrm{3}} } \\ $$
Commented by mathmax by abdo last updated on 16/May/20

$${I}\:=\int_{−\infty} ^{+\infty} \:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{4}\right)^{\mathrm{3}} }\:\Rightarrow\:{I}\:=\int_{−\infty} ^{+\infty} \:\frac{{dx}}{\left(\left({x}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{3}\right)^{\mathrm{3}} } \\ $$$$=_{{x}+\mathrm{1}\:=\sqrt{\mathrm{3}}{t}} \:\:\:\:\int_{−\infty} ^{+\infty} \:\frac{\sqrt{\mathrm{3}}{dt}}{\mathrm{27}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} }\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{27}}\:\int_{−\infty} ^{+\infty} \:\frac{{dt}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$${let}\:\varphi\left({z}\right)\:=\frac{\mathrm{1}}{\left({z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} }\:\Rightarrow\varphi\left({z}\right)\:=\frac{\mathrm{1}}{\left({z}−{i}\right)^{\mathrm{3}} \left({z}+{i}\right)^{\mathrm{3}} }\:{so}\:{the}\:{poles}\:{of}\:\varphi\:{are} \\ $$$${i}\:{and}\:−{i}\:\:\left({triples}\right){and}\:\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{i}\right) \\ $$$${Res}\left(\varphi,{i}\right)\:={lim}_{{z}\rightarrow{i}} \:\:\:\frac{\mathrm{1}}{\left(\mathrm{3}−\mathrm{1}\right)!}\left\{\left({z}−{i}\right)^{\mathrm{3}} \:\varphi\left({z}\right)\right\}^{\left(\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{lim}_{{z}\rightarrow{i}} \:\:\:\left\{\left({z}+{i}\right)^{−\mathrm{3}} \right\}^{\left(\mathrm{2}\right)} \:=\frac{\mathrm{1}}{\mathrm{2}}{lim}_{{z}\rightarrow{i}} \:\:\left\{−\mathrm{3}\left({z}+{i}\right)^{−\mathrm{4}} \right\}^{\left(\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{lim}_{{z}\rightarrow{i}} \:\:\:\mathrm{12}\:\left({z}+{i}\right)^{−\mathrm{5}} \:=\mathrm{6}\:\left(\mathrm{2}{i}\right)^{−\mathrm{5}} \:=\frac{\mathrm{6}}{\left(\mathrm{2}{i}\right)^{\mathrm{5}} }\:=\frac{\mathrm{6}}{\mathrm{32}\:{i}}\:=\frac{\mathrm{3}}{\mathrm{16}{i}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi×\frac{\mathrm{3}}{\mathrm{16}{i}}\:=\frac{\mathrm{3}\pi}{\mathrm{8}}\:\Rightarrow\:{I}\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{27}}×\frac{\mathrm{3}\pi}{\mathrm{8}}\:=\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{72}} \\ $$$$\bigstar\:{I}\:=\:\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{72}}\bigstar \\ $$
Answered by Ar Brandon last updated on 15/May/20
![L_n =∫((Ax+B)/((x^2 +px+q)^n ))dx⇒L_n =(B−((Ap)/2))∫_(−∞) ^(+∞) (1/([(x+(p/2))^2 +((√(q−(p^2 /4))))^2 ]^n ))dx A=0, B=1, p=2, q=4, n=3 ⇒L_3 =∫_(−∞) ^(+∞) (dx/((x^2 +2x+4)^3 ))=∫_(−∞) ^(+∞) (dx/([(x+1)^2 +((√3))^2 ]^3 )) J_n =∫_(−∞) ^(+∞) (1/([x^2 +u^2 ]^n ))dx⇒J_n =((2n−3)/(2u^2 (n−1)))J_(n−1) J_1 =∫_(−∞) ^(+∞) (dx/((x+1)^2 +((√3))^2 ))=((√3)/3)⌊tan^(−1) [((x+1)/( (√3)))]⌋_(−∞) ^(+∞) =((π(√3))/3) J_2 =((π(√3))/(18))⇒J_3 =(3/(12))∙((π(√3))/(18))=((π(√3))/(72)) ∫_(−∞) ^(+∞) (dx/((x^2 +2x+4)^3 ))=((π(√3))/(72))](https://www.tinkutara.com/question/Q93884.png)
$$\mathrm{L}_{\mathrm{n}} =\int\frac{\mathrm{Ax}+\mathrm{B}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{px}+\mathrm{q}\right)^{\mathrm{n}} }\mathrm{dx}\Rightarrow\mathrm{L}_{\mathrm{n}} =\left(\mathrm{B}−\frac{\mathrm{Ap}}{\mathrm{2}}\right)\int_{−\infty} ^{+\infty} \frac{\mathrm{1}}{\left[\left(\mathrm{x}+\frac{\mathrm{p}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{q}−\frac{\mathrm{p}^{\mathrm{2}} }{\mathrm{4}}}\right)^{\mathrm{2}} \right]^{\mathrm{n}} }\mathrm{dx} \\ $$$$\mathrm{A}=\mathrm{0},\:\mathrm{B}=\mathrm{1},\:\mathrm{p}=\mathrm{2},\:\mathrm{q}=\mathrm{4},\:\mathrm{n}=\mathrm{3} \\ $$$$\Rightarrow\mathrm{L}_{\mathrm{3}} =\int_{−\infty} ^{+\infty} \frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{4}\right)^{\mathrm{3}} }=\int_{−\infty} ^{+\infty} \frac{\mathrm{dx}}{\left[\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \right]^{\mathrm{3}} } \\ $$$$\mathrm{J}_{\mathrm{n}} =\int_{−\infty} ^{+\infty} \frac{\mathrm{1}}{\left[\mathrm{x}^{\mathrm{2}} +\mathrm{u}^{\mathrm{2}} \right]^{\mathrm{n}} }\mathrm{dx}\Rightarrow\mathrm{J}_{\mathrm{n}} =\frac{\mathrm{2n}−\mathrm{3}}{\mathrm{2u}^{\mathrm{2}} \left(\mathrm{n}−\mathrm{1}\right)}\mathrm{J}_{\mathrm{n}−\mathrm{1}} \\ $$$$\mathrm{J}_{\mathrm{1}} =\int_{−\infty} ^{+\infty} \frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\lfloor\mathrm{tan}^{−\mathrm{1}} \left[\frac{\mathrm{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right]\rfloor_{−\infty} ^{+\infty} =\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$$\mathrm{J}_{\mathrm{2}} =\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{18}}\Rightarrow\mathrm{J}_{\mathrm{3}} =\frac{\mathrm{3}}{\mathrm{12}}\centerdot\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{18}}=\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{72}} \\ $$$$\int_{−\infty} ^{+\infty} \frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{4}\right)^{\mathrm{3}} }=\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{72}} \\ $$
Commented by Ar Brandon last updated on 15/May/20
In case of necessity please check my solution to Q.93639 for Ln and Jn ��
Commented by mathmax by abdo last updated on 16/May/20

$${thank}\:{you}\:{sir}\:. \\ $$
Commented by Ar Brandon last updated on 16/May/20
cheers ��
