Question Number 144216 by Mathspace last updated on 23/Jun/21
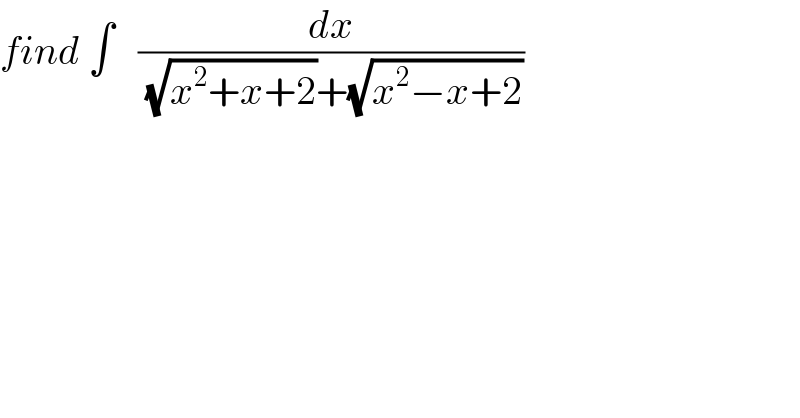
$${find}\:\int\:\:\:\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{2}}+\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{2}}} \\ $$
Answered by bemath last updated on 23/Jun/21
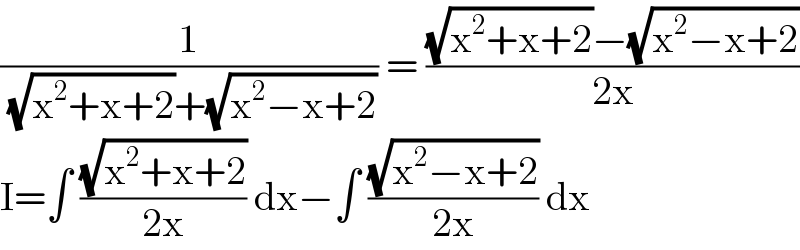
$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{2}}+\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{2}}}\:=\:\frac{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{2}}−\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{2}}}{\mathrm{2x}} \\ $$$$\mathrm{I}=\int\:\frac{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{2}}}{\mathrm{2x}}\:\mathrm{dx}−\int\:\frac{\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{2}}}{\mathrm{2x}}\:\mathrm{dx} \\ $$
