Menu Close

find-dx-x-2-x-x-2-2x-3-

Tinku Tara 0 Comments
Pin




Question Number 58220 by maxmathsup by imad last updated on 20/Apr/19
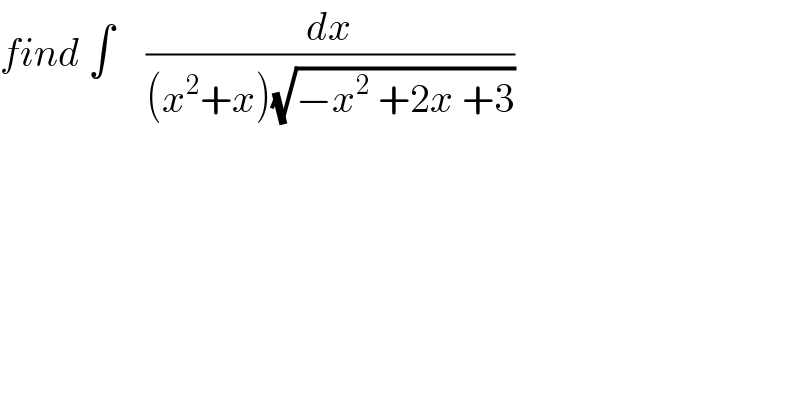
find ∫ (dx/((x^2 +x)(√(−x^2 +2x +3))))
$${find}\:\int\:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} +{x}\right)\sqrt{−{x}^{\mathrm{2}} \:+\mathrm{2}{x}\:+\mathrm{3}}} \\ $$$$ \\ $$
Answered by tanmay last updated on 20/Apr/19
−x^2 −x+3x+3 −x(x+1)+3(x+1) (x+1)(3−x) t^2 =x+1 dx=2tdt ∫(dx/(x(x+1)(√((x+1)(3−x))))) ∫((2tdt)/((t^2 −1)t^2 (√(t^2 (3−t^2 +1))))) ∫((2dt)/((t^2 −1)t^2 (√(4−t^2 )))) 2∫((t^2 −(t^2 −1))/(t^2 (t^2 −1)(√(4−t^2 ))))dt 2∫(dt/((t^2 −1)(√(4−t^2 ))))−2∫(dt/(t^2 (√(4−t^2 )) )) 2I_1 −2I_2 I_1 =∫(dt/((t^2 −1)(√(4−t^2 )))) a^2 =((4−t^2 )/(t^2 −1))→a^2 t^2 −a^2 =4−t^2 t^2 (a^2 +1)=a^2 +4 t^2 =((a^2 +4)/(a^2 +1)) 2tdt=(((a^2 +1)(2a)−(a^2 +4)(2a))/((a^2 +1)^2 ))da 2tdt=((2a^3 +2a−2a^3 −8a)/((a^2 +1)^2 ))da tdt=((−3ada)/((a^2 +1)^2 )) ∫((−3ada)/( (√((a^2 +4)/(a^2 +1)))×(a^2 +1)^2 ))×(1/((((a^2 +4)/(a^2 +1))−1)(√(4−(((a^2 +4)/(a^2 +1))))))) ∫((−3ada)/( (√(a^2 +4)) ))×(((√(a^2 +1)) )/((a^2 +1)^2 ))×(((a^2 +1))/(3(√((4a^2 +4−a^2 −4)/(a^2 +1))))) ∫((−3ada)/( (√(a^2 +4))))×(1/(3(√3) a)) ((−1)/( (√3)))∫(da/( (√(a^2 +4))))→{((−1)/( (√3)))ln(a+(√(a^2 +4)) )} so 2I_1 =((−2)/( (√3)))ln((√((4−t^2 )/(t^2 −1))) +(√(((4−t^2 )/(t^2 −1))+4)) ) =((−2)/( (√3)))ln((((√(4−t^2 )) +t(√3))/( (√(t^2 −1)) )))←value of I_1 lengthy problem wait for I_2 I_2 =∫(dt/(t^2 (√(4−t^2 )) )) t=2sinθ ∫((2cosθdθ)/(4sin^2 θ×2cosθ)) =(1/2)∫cosec^2 θdθ =((−cotθ)/2)=((−1)/2)((((√(4−t^2 )) )/t))←value of I_2 so complete answdr is 2I_1 −2I_2 2×((−2)/( (√3)))ln((((√(4−t^2 )) +t(√3))/( (√(t^2 −1)))))−2×((−1)/2)(((√(4−t^2 ))/t))+c t^2 =x+1 =((−4)/( (√3)))ln((((√(3−x)) +(√(3(x+1))) )/( (√x))))+(((√(3−x))/( (√(x+1)))))+c pls check...
$$−{x}^{\mathrm{2}} −{x}+\mathrm{3}{x}+\mathrm{3} \\ $$$$−{x}\left({x}+\mathrm{1}\right)+\mathrm{3}\left({x}+\mathrm{1}\right) \\ $$$$\left({x}+\mathrm{1}\right)\left(\mathrm{3}−{x}\right) \\ $$$${t}^{\mathrm{2}} ={x}+\mathrm{1}\:\:{dx}=\mathrm{2}{tdt} \\ $$$$\int\frac{{dx}}{{x}\left({x}+\mathrm{1}\right)\sqrt{\left({x}+\mathrm{1}\right)\left(\mathrm{3}−{x}\right)}} \\ $$$$\int\frac{\mathrm{2}{tdt}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right){t}^{\mathrm{2}} \sqrt{{t}^{\mathrm{2}} \left(\mathrm{3}−{t}^{\mathrm{2}} +\mathrm{1}\right)}} \\ $$$$\int\frac{\mathrm{2}{dt}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right){t}^{\mathrm{2}} \sqrt{\mathrm{4}−{t}^{\mathrm{2}} }} \\ $$$$\mathrm{2}\int\frac{{t}^{\mathrm{2}} −\left({t}^{\mathrm{2}} −\mathrm{1}\right)}{{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{\mathrm{4}−{t}^{\mathrm{2}} }}{dt} \\ $$$$\mathrm{2}\int\frac{{dt}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{\mathrm{4}−{t}^{\mathrm{2}} }}−\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{2}} \sqrt{\mathrm{4}−{t}^{\mathrm{2}} }\:} \\ $$$$\mathrm{2}{I}_{\mathrm{1}} −\mathrm{2}{I}_{\mathrm{2}} \\ $$$${I}_{\mathrm{1}} =\int\frac{{dt}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{\mathrm{4}−{t}^{\mathrm{2}} }} \\ $$$${a}^{\mathrm{2}} =\frac{\mathrm{4}−{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} −\mathrm{1}}\rightarrow{a}^{\mathrm{2}} {t}^{\mathrm{2}} −{a}^{\mathrm{2}} =\mathrm{4}−{t}^{\mathrm{2}} \\ $$$${t}^{\mathrm{2}} \left({a}^{\mathrm{2}} +\mathrm{1}\right)={a}^{\mathrm{2}} +\mathrm{4} \\ $$$${t}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} +\mathrm{4}}{{a}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{2}{tdt}=\frac{\left({a}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{2}{a}\right)−\left({a}^{\mathrm{2}} +\mathrm{4}\right)\left(\mathrm{2}{a}\right)}{\left({a}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{da} \\ $$$$\mathrm{2}{tdt}=\frac{\mathrm{2}{a}^{\mathrm{3}} +\mathrm{2}{a}−\mathrm{2}{a}^{\mathrm{3}} −\mathrm{8}{a}}{\left({a}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{da} \\ $$$${tdt}=\frac{−\mathrm{3}{ada}}{\left({a}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\int\frac{−\mathrm{3}{ada}}{\:\sqrt{\frac{{a}^{\mathrm{2}} +\mathrm{4}}{{a}^{\mathrm{2}} +\mathrm{1}}}×\left({a}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }×\frac{\mathrm{1}}{\left(\frac{{a}^{\mathrm{2}} +\mathrm{4}}{{a}^{\mathrm{2}} +\mathrm{1}}−\mathrm{1}\right)\sqrt{\mathrm{4}−\left(\frac{{a}^{\mathrm{2}} +\mathrm{4}}{{a}^{\mathrm{2}} +\mathrm{1}}\right)}} \\ $$$$\int\frac{−\mathrm{3}{ada}}{\:\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}\:}×\frac{\sqrt{{a}^{\mathrm{2}} +\mathrm{1}}\:}{\left({a}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }×\frac{\left({a}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{3}\sqrt{\frac{\mathrm{4}{a}^{\mathrm{2}} +\mathrm{4}−{a}^{\mathrm{2}} −\mathrm{4}}{{a}^{\mathrm{2}} +\mathrm{1}}}} \\ $$$$\int\frac{−\mathrm{3}{ada}}{\:\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}×\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{3}}\:{a}} \\ $$$$\frac{−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\int\frac{{da}}{\:\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}}\rightarrow\left\{\frac{−\mathrm{1}}{\:\sqrt{\mathrm{3}}}{ln}\left({a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{4}}\:\right)\right\} \\ $$$${so}\:\mathrm{2}{I}_{\mathrm{1}} =\frac{−\mathrm{2}}{\:\sqrt{\mathrm{3}}}{ln}\left(\sqrt{\frac{\mathrm{4}−{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} −\mathrm{1}}}\:+\sqrt{\frac{\mathrm{4}−{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} −\mathrm{1}}+\mathrm{4}}\:\:\right) \\ $$$$=\frac{−\mathrm{2}}{\:\sqrt{\mathrm{3}}}{ln}\left(\frac{\sqrt{\mathrm{4}−{t}^{\mathrm{2}} }\:+{t}\sqrt{\mathrm{3}}}{\:\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\:}\right)\leftarrow{value}\:{of}\:{I}_{\mathrm{1}} \\ $$$${lengthy}\:{problem}\:{wait}\:{for}\:{I}_{\mathrm{2}} \\ $$$${I}_{\mathrm{2}} =\int\frac{{dt}}{{t}^{\mathrm{2}} \sqrt{\mathrm{4}−{t}^{\mathrm{2}} }\:}\:\: \\ $$$${t}=\mathrm{2}{sin}\theta\: \\ $$$$\int\frac{\mathrm{2}{cos}\theta{d}\theta}{\mathrm{4}{sin}^{\mathrm{2}} \theta×\mathrm{2}{cos}\theta} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int{cosec}^{\mathrm{2}} \theta{d}\theta \\ $$$$=\frac{−{cot}\theta}{\mathrm{2}}=\frac{−\mathrm{1}}{\mathrm{2}}\left(\frac{\sqrt{\mathrm{4}−{t}^{\mathrm{2}} }\:}{{t}}\right)\leftarrow{value}\:{of}\:{I}_{\mathrm{2}} \\ $$$$ \\ $$$${so}\:{complete}\:{answdr}\:{is}\:\mathrm{2}{I}_{\mathrm{1}} −\mathrm{2}{I}_{\mathrm{2}} \\ $$$$\mathrm{2}×\frac{−\mathrm{2}}{\:\sqrt{\mathrm{3}}}{ln}\left(\frac{\sqrt{\mathrm{4}−{t}^{\mathrm{2}} }\:+{t}\sqrt{\mathrm{3}}}{\:\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}}\right)−\mathrm{2}×\frac{−\mathrm{1}}{\mathrm{2}}\left(\frac{\sqrt{\mathrm{4}−{t}^{\mathrm{2}} }}{{t}}\right)+{c} \\ $$$${t}^{\mathrm{2}} ={x}+\mathrm{1} \\ $$$$=\frac{−\mathrm{4}}{\:\sqrt{\mathrm{3}}}{ln}\left(\frac{\sqrt{\mathrm{3}−{x}}\:+\sqrt{\mathrm{3}\left({x}+\mathrm{1}\right)}\:}{\:\sqrt{{x}}}\right)+\left(\frac{\sqrt{\mathrm{3}−{x}}}{\:\sqrt{{x}+\mathrm{1}}}\right)+{c} \\ $$$${pls}\:{check}… \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *