Menu Close

find-dx-x-x-1-x-2-x-

Tinku Tara 0 Comments
Pin




Question Number 122205 by mathmax by abdo last updated on 14/Nov/20
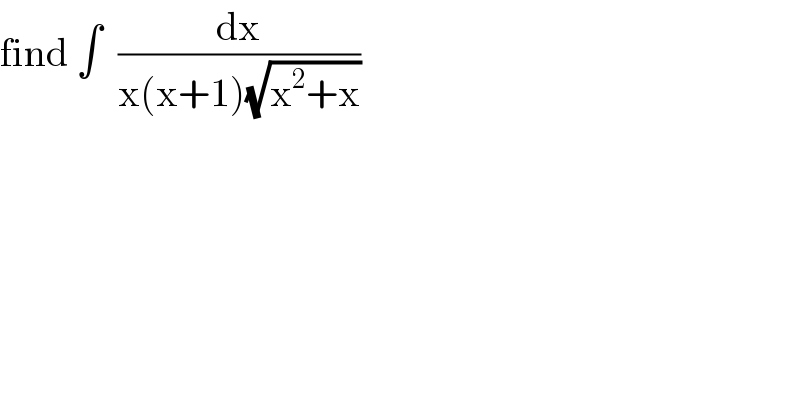
find ∫ (dx/(x(x+1)(√(x^2 +x))))
$$\mathrm{find}\:\int\:\:\frac{\mathrm{dx}}{\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}} \\ $$
Commented by liberty last updated on 15/Nov/20
∫ (dx/((x^2 +x)^(3/2) )) = ∫ (dx/(x^3 (1+x^(−1) )^(3/2) )) = ∫ ((x^(−2) dx)/(x(1+x^(−1) )^(3/2) )) ; [ u^(2/3) = 1+(1/x) ] ⇒ [ (2/3)u^(−(1/3)) du = −x^(−2) dx ] J = ∫ (u^(2/3) −1)(−(2/3)u^(−(1/3)) du)((1/u)) J= −(2/3)∫ (u^(2/3) −1)(u^(−(4/3)) ) du J=−(2/3)∫ (u^(−(2/3)) −u^(−(4/3)) ) du J = −(2/3)[ 3u^(1/3) +3u^(−(1/3)) ] + c J = −2(√((x+1)/x))−2(√(x/(x+1))) + c J= −2(((x+1+x)/( (√(x^2 +x)))))+ c = −((4x+2)/( (√(x^2 +x)))) + c
$$\:\int\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\:=\:\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{3}} \left(\mathrm{1}+\mathrm{x}^{−\mathrm{1}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$\:=\:\int\:\frac{\mathrm{x}^{−\mathrm{2}} \mathrm{dx}}{\mathrm{x}\left(\mathrm{1}+\mathrm{x}^{−\mathrm{1}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\:;\:\left[\:\mathrm{u}^{\frac{\mathrm{2}}{\mathrm{3}}} \:=\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}\:\right] \\ $$$$\Rightarrow\:\left[\:\frac{\mathrm{2}}{\mathrm{3}}\mathrm{u}^{−\frac{\mathrm{1}}{\mathrm{3}}} \:\mathrm{du}\:=\:−\mathrm{x}^{−\mathrm{2}} \:\mathrm{dx}\:\right] \\ $$$$\mathrm{J}\:=\:\int\:\left(\mathrm{u}^{\frac{\mathrm{2}}{\mathrm{3}}} −\mathrm{1}\right)\left(−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{u}^{−\frac{\mathrm{1}}{\mathrm{3}}} \:\mathrm{du}\right)\left(\frac{\mathrm{1}}{\mathrm{u}}\right) \\ $$$$\mathrm{J}=\:−\frac{\mathrm{2}}{\mathrm{3}}\int\:\left(\mathrm{u}^{\frac{\mathrm{2}}{\mathrm{3}}} −\mathrm{1}\right)\left(\mathrm{u}^{−\frac{\mathrm{4}}{\mathrm{3}}} \right)\:\mathrm{du} \\ $$$$\mathrm{J}=−\frac{\mathrm{2}}{\mathrm{3}}\int\:\left(\mathrm{u}^{−\frac{\mathrm{2}}{\mathrm{3}}} −\mathrm{u}^{−\frac{\mathrm{4}}{\mathrm{3}}} \right)\:\mathrm{du}\: \\ $$$$\mathrm{J}\:=\:−\frac{\mathrm{2}}{\mathrm{3}}\left[\:\mathrm{3u}^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{3u}^{−\frac{\mathrm{1}}{\mathrm{3}}} \:\right]\:+\:\mathrm{c}\: \\ $$$$\mathrm{J}\:=\:−\mathrm{2}\sqrt{\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}}}−\mathrm{2}\sqrt{\frac{\mathrm{x}}{\mathrm{x}+\mathrm{1}}}\:+\:\mathrm{c}\: \\ $$$$\mathrm{J}=\:\:−\mathrm{2}\left(\frac{\mathrm{x}+\mathrm{1}+\mathrm{x}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}}\right)+\:\mathrm{c}\:=\:−\frac{\mathrm{4x}+\mathrm{2}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}}\:+\:\mathrm{c} \\ $$
Commented by benjo_mathlover last updated on 15/Nov/20
let J(x)=−((4x+2)/( (√(x^2 +x)))) ((dJ(x))/dx) = − [ ((4(√(x^2 +x))−(4x+2)(((2x+1)/(2(√(x^2 +x))))))/(x^2 +x)) ] = − [((4(√(x^2 +x))−(((2x+1)^2 )/( (√(x^2 +x)))))/(x^2 +x)) ] = − [ ((4x^2 +4x−4x^2 −4x−1)/((x^2 +x)(√(x^2 +x)))) ] = (1/(x(x+1)(√(x^2 +x)))) correct sir Liberty.
$${let}\:{J}\left({x}\right)=−\frac{\mathrm{4}{x}+\mathrm{2}}{\:\sqrt{{x}^{\mathrm{2}} +{x}}} \\ $$$$\:\frac{{dJ}\left({x}\right)}{{dx}}\:=\:−\:\left[\:\frac{\mathrm{4}\sqrt{{x}^{\mathrm{2}} +{x}}−\left(\mathrm{4}{x}+\mathrm{2}\right)\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{x}}}\right)}{{x}^{\mathrm{2}} +{x}}\:\right] \\ $$$$\:\:\:\:\:\:=\:−\:\left[\frac{\mathrm{4}\sqrt{{x}^{\mathrm{2}} +{x}}−\frac{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} }{\:\sqrt{{x}^{\mathrm{2}} +{x}}}}{{x}^{\mathrm{2}} +{x}}\:\right] \\ $$$$\:\:\:\:\:\:=\:−\:\left[\:\frac{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{x}−\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{1}}{\left({x}^{\mathrm{2}} +{x}\right)\sqrt{{x}^{\mathrm{2}} +{x}}}\:\right] \\ $$$$\:\:\:\:\:\:=\:\frac{\mathrm{1}}{{x}\left({x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +{x}}} \\ $$$${correct}\:{sir}\:{Liberty}. \\ $$
Answered by TANMAY PANACEA last updated on 14/Nov/20
∫(((x+1)−x)/(x(x+1)(√(x^2 +x))))dx ∫(dx/(x(√(x^2 +x))))−∫(dx/((x+1)(√(x^2 +x)) )) a=(1/x)→dx=((−1)/a^2 ) da b=(1/(x+1))→dx=−(1/b^2 )db ∫((−da)/(a^2 ×(1/a)×(√((1/a^2 )+(1/a)))))−∫((−db)/(b^2 ×(1/b)(√(((1/b)−1)^2 +((1/b)−1))))) ∫((−da)/( (√(1+a^2 ))))−∫(db/(b×(√((1/b^2 )−(2/b)+1+(1/b)−1)))) ∫((−da)/( (√(1+a^2 ))))−∫(db/( (√(1−b)))) ∫((−da)/( (√(1+a^2 ))))+∫((d(1−b))/( (√(1−b)))) −ln(a+(√(1+a^2 )) )+(((1−b)^(1/2) )/(1/2))+C −ln((1/x)+(√(1+(1/x^2 ))) +2(1−(1/(x+1)))^(1/2) +c
$$\int\frac{\left({x}+\mathrm{1}\right)−{x}}{{x}\left({x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +{x}}}{dx} \\ $$$$\int\frac{{dx}}{{x}\sqrt{{x}^{\mathrm{2}} +{x}}}−\int\frac{{dx}}{\left({x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +{x}}\:} \\ $$$${a}=\frac{\mathrm{1}}{{x}}\rightarrow{dx}=\frac{−\mathrm{1}}{{a}^{\mathrm{2}} }\:{da}\:\:\:\:\:{b}=\frac{\mathrm{1}}{{x}+\mathrm{1}}\rightarrow{dx}=−\frac{\mathrm{1}}{{b}^{\mathrm{2}} }{db} \\ $$$$\int\frac{−{da}}{{a}^{\mathrm{2}} ×\frac{\mathrm{1}}{{a}}×\sqrt{\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{a}}}}−\int\frac{−{db}}{{b}^{\mathrm{2}} ×\frac{\mathrm{1}}{{b}}\sqrt{\left(\frac{\mathrm{1}}{{b}}−\mathrm{1}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{{b}}−\mathrm{1}\right)}} \\ $$$$\int\frac{−{da}}{\:\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}−\int\frac{{db}}{{b}×\sqrt{\frac{\mathrm{1}}{{b}^{\mathrm{2}} }−\frac{\mathrm{2}}{{b}}+\mathrm{1}+\frac{\mathrm{1}}{{b}}−\mathrm{1}}} \\ $$$$\int\frac{−{da}}{\:\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}−\int\frac{{db}}{\:\sqrt{\mathrm{1}−{b}}} \\ $$$$\int\frac{−{da}}{\:\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}+\int\frac{{d}\left(\mathrm{1}−{b}\right)}{\:\sqrt{\mathrm{1}−{b}}} \\ $$$$−{ln}\left({a}+\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }\:\right)+\frac{\left(\mathrm{1}−{b}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{\frac{\mathrm{1}}{\mathrm{2}}}+{C} \\ $$$$−{ln}\left(\frac{\mathrm{1}}{{x}}+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\:+\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}+\mathrm{1}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} +{c}\right. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *