Question Number 84178 by www.abhisheksoni39@gmail.com last updated on 10/Mar/20
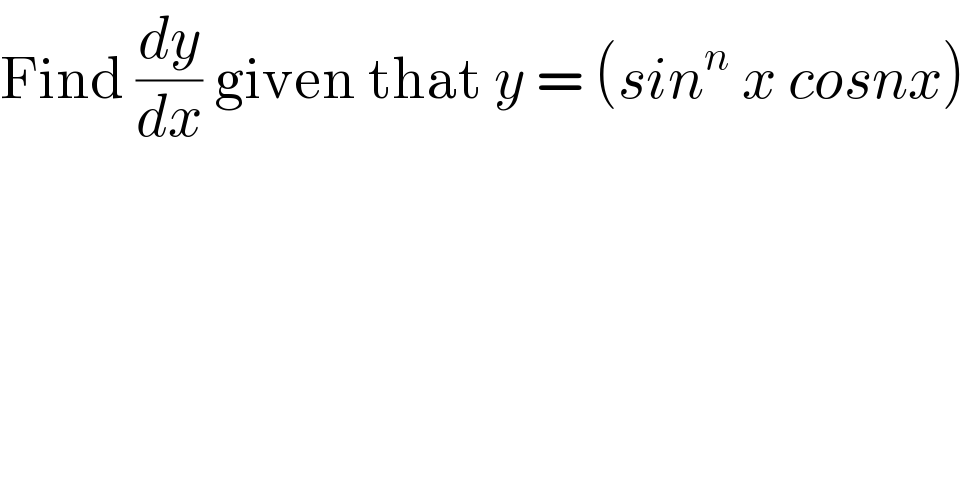
$$\mathrm{Find}\:\frac{{dy}}{{dx}}\:\mathrm{given}\:\mathrm{that}\:{y}\:=\:\left({sin}^{{n}} \:{x}\:{cosnx}\right) \\ $$
Answered by john santu last updated on 10/Mar/20
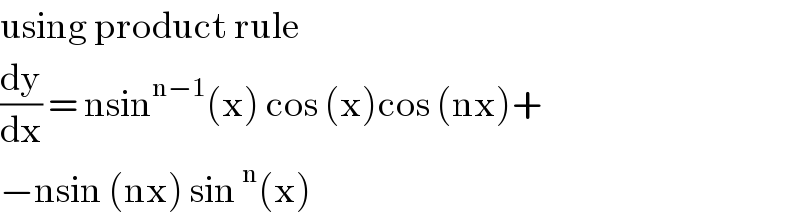
$$\mathrm{using}\:\mathrm{product}\:\mathrm{rule} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{nsin}^{\mathrm{n}−\mathrm{1}} \left(\mathrm{x}\right)\:\mathrm{cos}\:\left(\mathrm{x}\right)\mathrm{cos}\:\left(\mathrm{nx}\right)+ \\ $$$$−\mathrm{nsin}\:\left(\mathrm{nx}\right)\:\mathrm{sin}\:^{\mathrm{n}} \left(\mathrm{x}\right)\: \\ $$
