Question Number 129727 by abdurehime last updated on 18/Jan/21
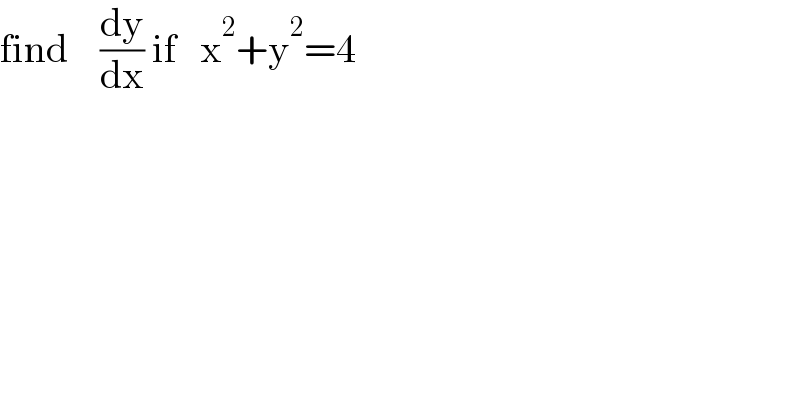
$$\mathrm{find}\:\:\:\:\frac{\mathrm{dy}}{\mathrm{dx}}\:\mathrm{if}\:\:\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\mathrm{4} \\ $$
Answered by Ar Brandon last updated on 18/Jan/21
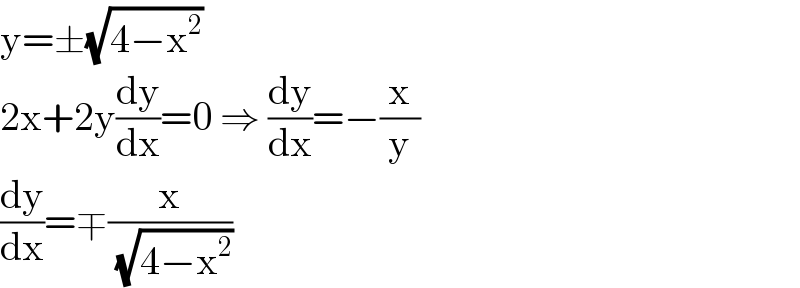
$$\mathrm{y}=\pm\sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{2x}+\mathrm{2y}\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{0}\:\Rightarrow\:\frac{\mathrm{dy}}{\mathrm{dx}}=−\frac{\mathrm{x}}{\mathrm{y}} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}=\mp\frac{\mathrm{x}}{\:\sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }} \\ $$
Answered by Adel last updated on 18/Jan/21
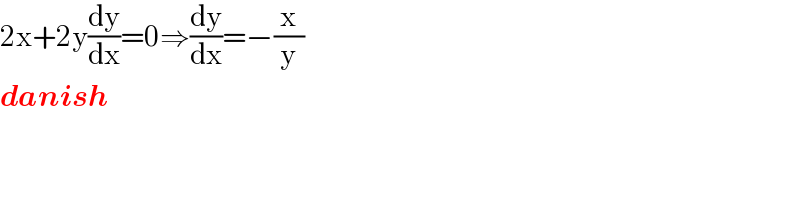
$$\mathrm{2x}+\mathrm{2y}\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{0}\Rightarrow\frac{\mathrm{dy}}{\mathrm{dx}}=−\frac{\mathrm{x}}{\mathrm{y}} \\ $$$$\boldsymbol{{danish}} \\ $$
