Find-dy-dx-of-2-x-y-2-2xy-x-y-C-

Question Number 97073 by naka3546 last updated on 06/Jun/20

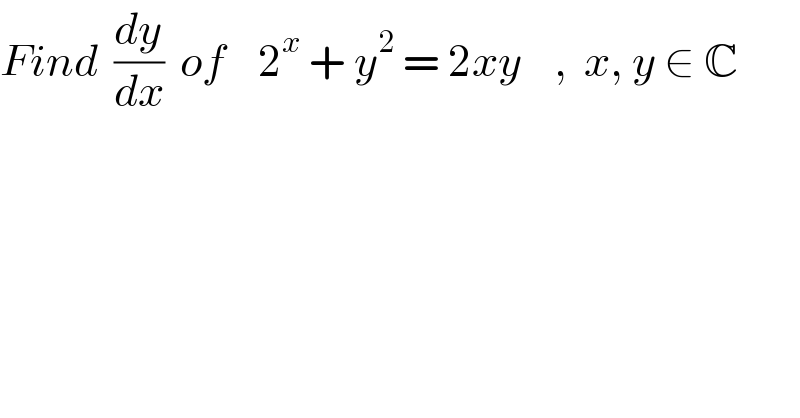
$${Find}\:\:\frac{{dy}}{{dx}}\:\:{of}\:\:\:\:\mathrm{2}^{{x}} \:+\:{y}^{\mathrm{2}} \:=\:\mathrm{2}{xy}\:\:\:\:,\:\:{x},\:{y}\:\in\:\mathbb{C} \\ $$

Commented by john santu last updated on 06/Jun/20

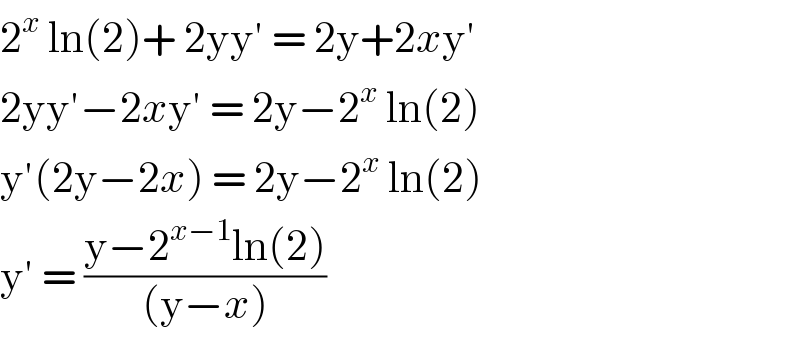
2^x ln(2)+ 2yy′ = 2y+2xy′ 2yy′−2xy′ = 2y−2^x ln(2) y′(2y−2x) = 2y−2^x ln(2) y′ = ((y−2^(x−1) ln(2))/((y−x)))

$$\mathrm{2}^{{x}} \:\mathrm{ln}\left(\mathrm{2}\right)+\:\mathrm{2yy}'\:=\:\mathrm{2y}+\mathrm{2}{x}\mathrm{y}' \\ $$$$\mathrm{2yy}'−\mathrm{2}{x}\mathrm{y}'\:=\:\mathrm{2y}−\mathrm{2}^{{x}} \:\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$\mathrm{y}'\left(\mathrm{2y}−\mathrm{2}{x}\right)\:=\:\mathrm{2y}−\mathrm{2}^{{x}} \:\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$\mathrm{y}'\:=\:\frac{\mathrm{y}−\mathrm{2}^{{x}−\mathrm{1}} \mathrm{ln}\left(\mathrm{2}\right)}{\left(\mathrm{y}−{x}\right)}\: \\ $$

Commented by mahdi last updated on 06/Jun/20

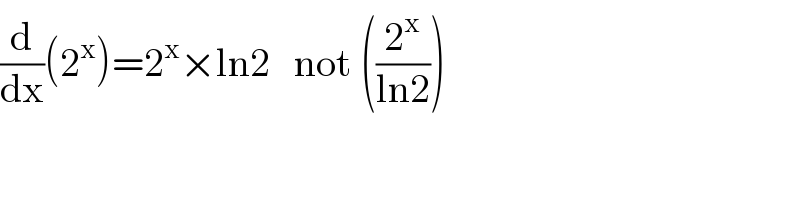
(d/dx)(2^x )=2^x ×ln2 not ((2^x /(ln2)))

$$\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{2}^{\mathrm{x}} \right)=\mathrm{2}^{\mathrm{x}} ×\mathrm{ln2}\:\:\:\mathrm{not}\:\left(\frac{\mathrm{2}^{\mathrm{x}} }{\mathrm{ln2}}\right) \\ $$

Commented by john santu last updated on 06/Jun/20

$$\mathrm{oo}\:\mathrm{sorry} \\ $$

Commented by Rasheed.Sindhi last updated on 06/Jun/20

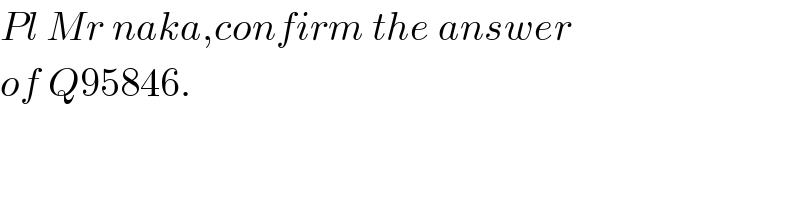
Pl Mr naka,confirm the answer of Q95846.

$${Pl}\:{Mr}\:{naka},{confirm}\:{the}\:{answer} \\ $$$${of}\:{Q}\mathrm{95846}. \\ $$

Answered by mahdi last updated on 06/Jun/20

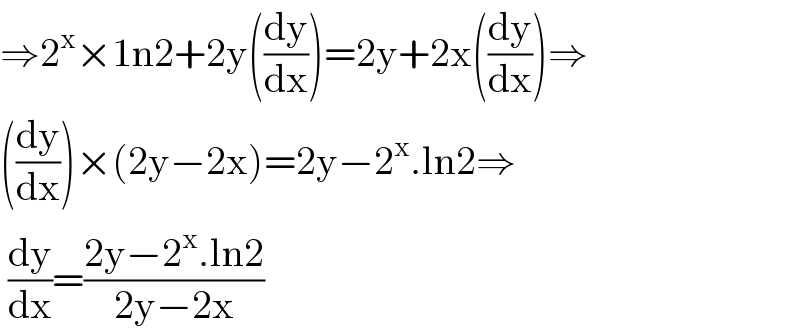
⇒2^x ×1n2+2y((dy/dx))=2y+2x((dy/dx))⇒ ((dy/dx))×(2y−2x)=2y−2^x .ln2⇒ (dy/dx)=((2y−2^x .ln2)/(2y−2x))

$$\Rightarrow\mathrm{2}^{\mathrm{x}} ×\mathrm{1n2}+\mathrm{2y}\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)=\mathrm{2y}+\mathrm{2x}\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)\Rightarrow \\ $$$$\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)×\left(\mathrm{2y}−\mathrm{2x}\right)=\mathrm{2y}−\mathrm{2}^{\mathrm{x}} .\mathrm{ln2}\Rightarrow \\ $$$$\:\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{2y}−\mathrm{2}^{\mathrm{x}} .\mathrm{ln2}}{\mathrm{2y}−\mathrm{2x}} \\ $$

Answered by Sourav mridha last updated on 06/Jun/20

⇒2^x ln(2)+2y(dy/dx)=2y+2x(dy/dx) ⇒(dy/dx)=((2y−2^x ln(2))/(2y−2x))=((2^x [1−xln(2)]+y^2 )/(2^x +y^2 −2x^2 )).

$$\Rightarrow\mathrm{2}^{\boldsymbol{{x}}} \boldsymbol{{ln}}\left(\mathrm{2}\right)+\mathrm{2}\boldsymbol{{y}}\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}=\mathrm{2}\boldsymbol{{y}}+\mathrm{2}\boldsymbol{{x}}\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}} \\ $$$$\Rightarrow\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}=\frac{\mathrm{2}\boldsymbol{{y}}−\mathrm{2}^{\boldsymbol{{x}}} \boldsymbol{{ln}}\left(\mathrm{2}\right)}{\mathrm{2}\boldsymbol{{y}}−\mathrm{2}\boldsymbol{{x}}}=\frac{\mathrm{2}^{\boldsymbol{{x}}} \left[\mathrm{1}−\boldsymbol{{xln}}\left(\mathrm{2}\right)\right]+\boldsymbol{\mathrm{y}}^{\mathrm{2}} }{\mathrm{2}^{\boldsymbol{\mathrm{x}}} +\boldsymbol{\mathrm{y}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{x}}^{\mathrm{2}} }. \\ $$

Answered by mathmax by abdo last updated on 06/Jun/20

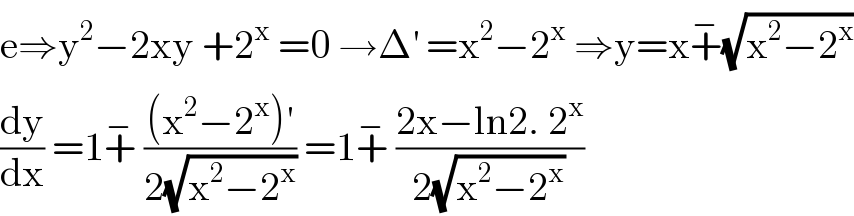
e⇒y^2 −2xy +2^x =0 →Δ^′ =x^2 −2^x ⇒y=x+^− (√(x^2 −2^x )) (dy/dx) =1+^− (((x^2 −2^x )^′ )/(2(√(x^2 −2^x )))) =1+^− ((2x−ln2. 2^x )/(2(√(x^2 −2^x ))))

$$\mathrm{e}\Rightarrow\mathrm{y}^{\mathrm{2}} −\mathrm{2xy}\:+\mathrm{2}^{\mathrm{x}} \:=\mathrm{0}\:\rightarrow\Delta^{'} \:=\mathrm{x}^{\mathrm{2}} −\mathrm{2}^{\mathrm{x}} \:\Rightarrow\mathrm{y}=\mathrm{x}\overset{−} {+}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{2}^{\mathrm{x}} } \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\mathrm{1}\overset{−} {+}\:\frac{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2}^{\mathrm{x}} \right)^{'} }{\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{2}^{\mathrm{x}} }}\:=\mathrm{1}\overset{−} {+}\:\frac{\mathrm{2x}−\mathrm{ln2}.\:\mathrm{2}^{\mathrm{x}} }{\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{2}^{\mathrm{x}} }} \\ $$

Facebook Tweet Pin

Find-dy-dx-of-2-x-y-2-2xy-x-y-C-

Leave a Reply Cancel reply