Question Number 61818 by Kunal12588 last updated on 09/Jun/19
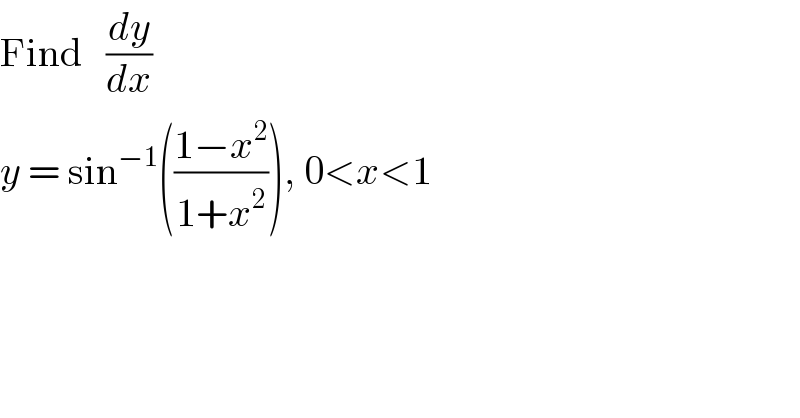
$$\mathrm{Find}\:\:\:\frac{{dy}}{{dx}}\:\: \\ $$$${y}\:=\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\right),\:\mathrm{0}<{x}<\mathrm{1} \\ $$
Commented by Prithwish sen last updated on 09/Jun/19
![(dy/dx) = (1/( (√(1−[(((1−x^2 ))/((1+x^2 )))]^2 )))) ((−2x(1+x^2 )−2x(1−x^2 ))/((1+x^2 )^2 )) =(((1+x^2 ))/(2x)) (((−4x))/((1+x^2 )^2 )) =((−2)/((1+x^2 )))](https://www.tinkutara.com/question/Q61819.png)
$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\left[\frac{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}\right]^{\mathrm{2}} }}\:\frac{−\mathrm{2x}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)−\mathrm{2x}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=\frac{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{2x}}\:\frac{\left(−\mathrm{4x}\right)}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=\frac{−\mathrm{2}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)} \\ $$
Commented by Kunal12588 last updated on 09/Jun/19
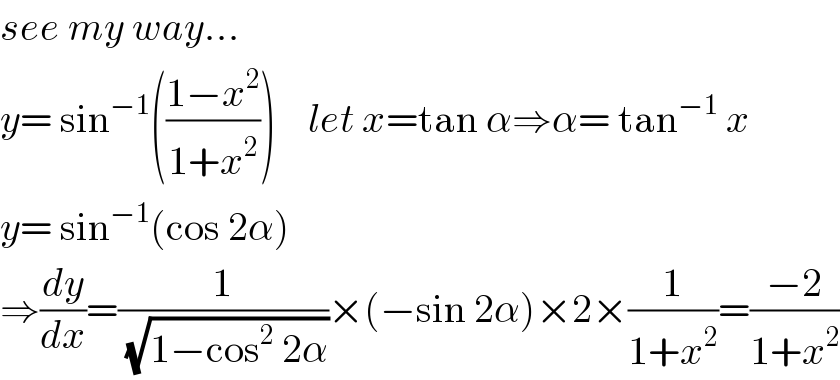
$${see}\:{my}\:{way}… \\ $$$${y}=\:\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\right)\:\:\:\:{let}\:{x}=\mathrm{tan}\:\alpha\Rightarrow\alpha=\:\mathrm{tan}^{−\mathrm{1}} \:{x} \\ $$$${y}=\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{cos}\:\mathrm{2}\alpha\right) \\ $$$$\Rightarrow\frac{{dy}}{{dx}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}\alpha}}×\left(−\mathrm{sin}\:\mathrm{2}\alpha\right)×\mathrm{2}×\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }=\frac{−\mathrm{2}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$
Commented by Prithwish sen last updated on 09/Jun/19

$$\mathrm{Beautiful} \\ $$
