Question Number 36441 by prof Abdo imad last updated on 02/Jun/18

$${find}\:\:\int\:\:\:\frac{{e}^{{tanx}} }{{cos}^{\mathrm{2}} {x}}{dx} \\ $$
Commented by prof Abdo imad last updated on 03/Jun/18
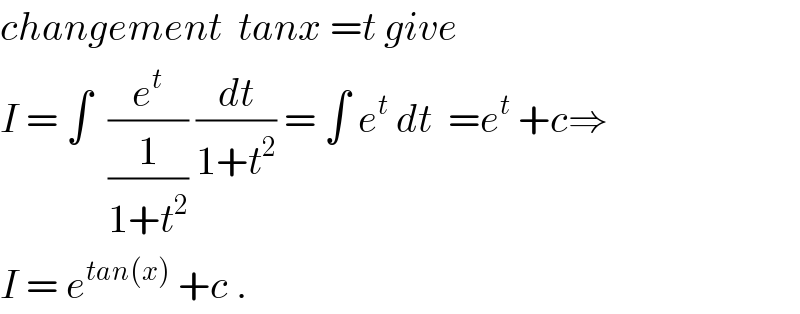
$${changement}\:\:{tanx}\:={t}\:{give} \\ $$$${I}\:=\:\int\:\:\frac{{e}^{{t}} }{\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\:\int\:{e}^{{t}} \:{dt}\:\:={e}^{{t}} \:+{c}\Rightarrow \\ $$$${I}\:=\:{e}^{{tan}\left({x}\right)} \:+{c}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 02/Jun/18
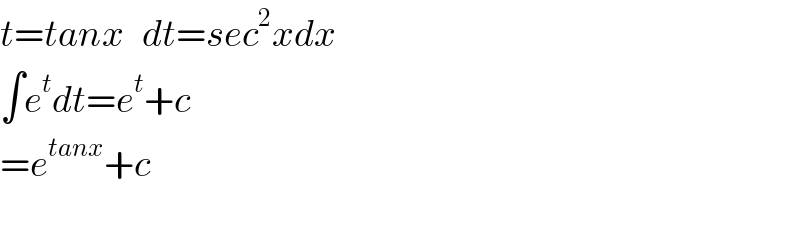
$${t}={tanx}\:\:\:{dt}={sec}^{\mathrm{2}} {xdx} \\ $$$$\int{e}^{{t}} {dt}={e}^{{t}} +{c} \\ $$$$={e}^{{tanx}} +{c} \\ $$$$ \\ $$
