Question Number 31104 by abdo imad last updated on 02/Mar/18
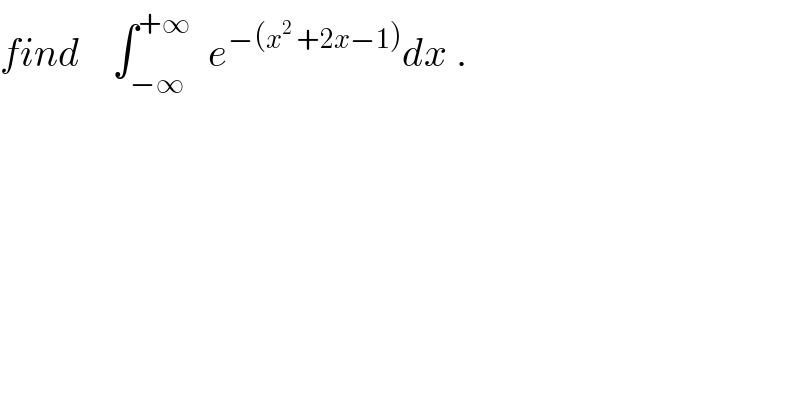
$${find}\:\:\:\:\int_{−\infty} ^{+\infty} \:\:{e}^{−\left({x}^{\mathrm{2}} \:+\mathrm{2}{x}−\mathrm{1}\right)} {dx}\:. \\ $$
Commented by abdo imad last updated on 03/Mar/18
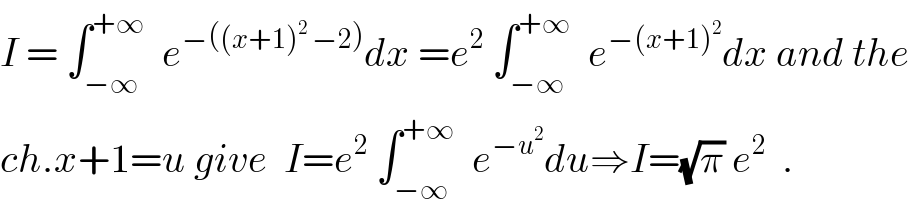
$${I}\:=\:\int_{−\infty} ^{+\infty} \:\:{e}^{−\left(\left({x}+\mathrm{1}\right)^{\mathrm{2}} \:−\mathrm{2}\right)} {dx}\:={e}^{\mathrm{2}} \:\int_{−\infty} ^{+\infty} \:\:{e}^{−\left({x}+\mathrm{1}\right)^{\mathrm{2}} } {dx}\:{and}\:{the} \\ $$$${ch}.{x}+\mathrm{1}={u}\:{give}\:\:{I}={e}^{\mathrm{2}} \:\int_{−\infty} ^{+\infty} \:\:{e}^{−{u}^{\mathrm{2}} } {du}\Rightarrow{I}=\sqrt{\pi}\:{e}^{\mathrm{2}} \:\:. \\ $$
