Question Number 29536 by math solver last updated on 09/Feb/18
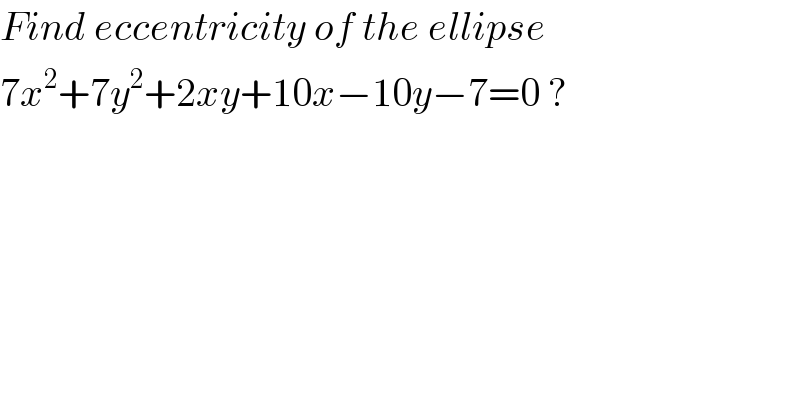
$${Find}\:{eccentricity}\:{of}\:{the}\:{ellipse} \\ $$$$\mathrm{7}{x}^{\mathrm{2}} +\mathrm{7}{y}^{\mathrm{2}} +\mathrm{2}{xy}+\mathrm{10}{x}−\mathrm{10}{y}−\mathrm{7}=\mathrm{0}\:? \\ $$
Commented by math solver last updated on 10/Feb/18

$${sir}\:,\:{i}\:{did}\:{this}\:{q}.\:{as}\:: \\ $$$${i}\:{rotated}\:{it}\:{by}\:\mathrm{45}^{{o}} \:{and}\:{then}\:{after} \\ $$$${converting}\:{to}\:{general}\:{eq}.\:{of}\:{ellipse} \\ $$$${i}\:{got}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}.\:{is}\:{my}\:{method}\:{is}\:{wrong} \\ $$$${or}\:{i}\:{did}\:{calculation}\:{mistake}. \\ $$
Commented by ajfour last updated on 10/Feb/18
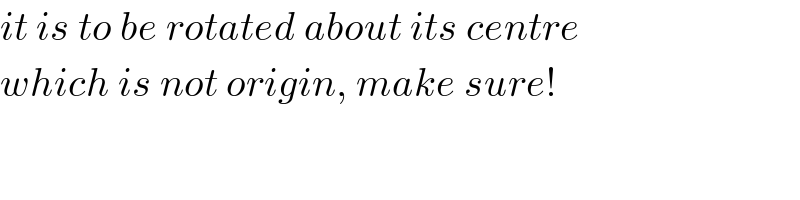
$${it}\:{is}\:{to}\:{be}\:{rotated}\:{about}\:{its}\:{centre} \\ $$$${which}\:{is}\:{not}\:{origin},\:{make}\:{sure}! \\ $$
Commented by ajfour last updated on 10/Feb/18
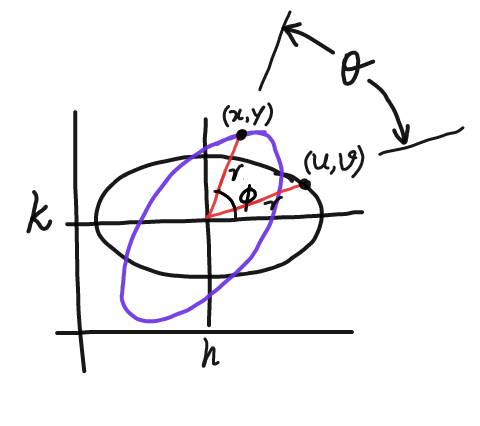
Commented by ajfour last updated on 10/Feb/18
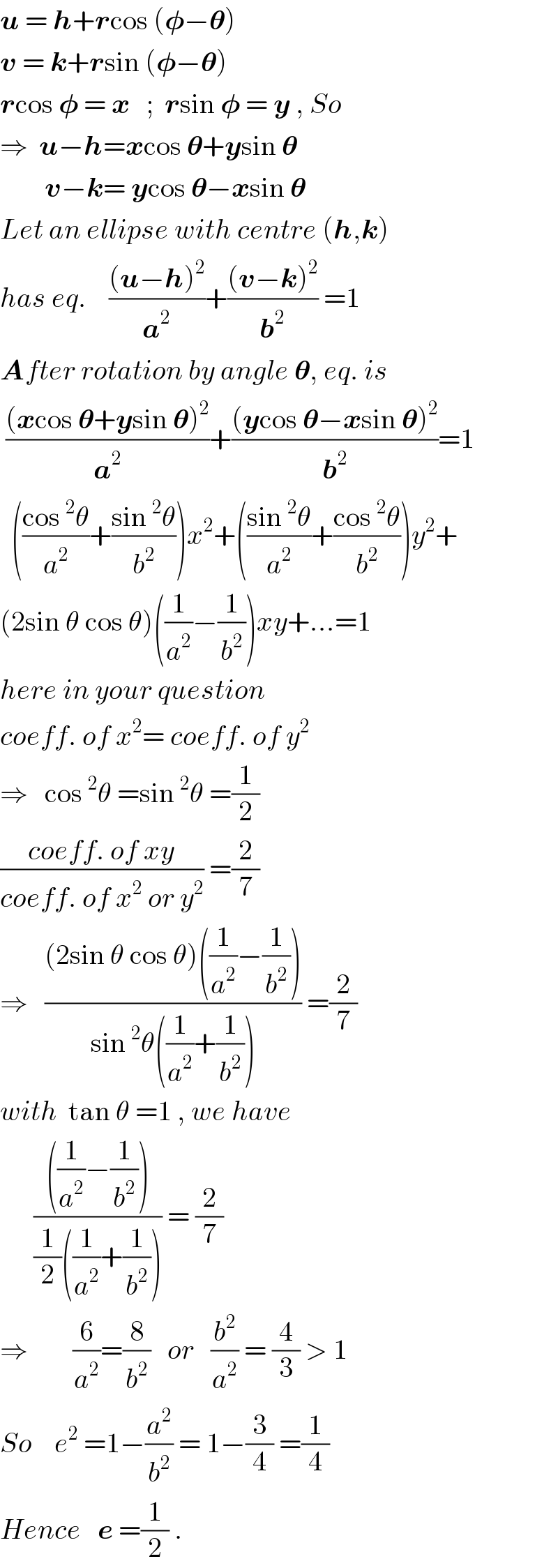
$$\boldsymbol{{u}}\:=\:\boldsymbol{{h}}+\boldsymbol{{r}}\mathrm{cos}\:\left(\boldsymbol{\phi}−\boldsymbol{\theta}\right) \\ $$$$\boldsymbol{{v}}\:=\:\boldsymbol{{k}}+\boldsymbol{{r}}\mathrm{sin}\:\left(\boldsymbol{\phi}−\boldsymbol{\theta}\right) \\ $$$$\boldsymbol{{r}}\mathrm{cos}\:\boldsymbol{\phi}\:=\:\boldsymbol{{x}}\:\:\:;\:\:\boldsymbol{{r}}\mathrm{sin}\:\boldsymbol{\phi}\:=\:\boldsymbol{{y}}\:,\:{So} \\ $$$$\Rightarrow\:\:\boldsymbol{{u}}−\boldsymbol{{h}}=\boldsymbol{{x}}\mathrm{cos}\:\boldsymbol{\theta}+\boldsymbol{{y}}\mathrm{sin}\:\boldsymbol{\theta} \\ $$$$\:\:\:\:\:\:\:\:\boldsymbol{{v}}−\boldsymbol{{k}}=\:\boldsymbol{{y}}\mathrm{cos}\:\boldsymbol{\theta}−\boldsymbol{{x}}\mathrm{sin}\:\boldsymbol{\theta} \\ $$$${Let}\:{an}\:{ellipse}\:{with}\:{centre}\:\left(\boldsymbol{{h}},\boldsymbol{{k}}\right) \\ $$$${has}\:{eq}.\:\:\:\:\frac{\left(\boldsymbol{{u}}−\boldsymbol{{h}}\right)^{\mathrm{2}} }{\boldsymbol{{a}}^{\mathrm{2}} }+\frac{\left(\boldsymbol{{v}}−\boldsymbol{{k}}\right)^{\mathrm{2}} }{\boldsymbol{{b}}^{\mathrm{2}} }\:=\mathrm{1} \\ $$$$\boldsymbol{{A}}{fter}\:{rotation}\:{by}\:{angle}\:\boldsymbol{\theta},\:{eq}.\:{is} \\ $$$$\:\frac{\left(\boldsymbol{{x}}\mathrm{cos}\:\boldsymbol{\theta}+\boldsymbol{{y}}\mathrm{sin}\:\boldsymbol{\theta}\right)^{\mathrm{2}} }{\boldsymbol{{a}}^{\mathrm{2}} }+\frac{\left(\boldsymbol{{y}}\mathrm{cos}\:\boldsymbol{\theta}−\boldsymbol{{x}}\mathrm{sin}\:\boldsymbol{\theta}\right)^{\mathrm{2}} }{\boldsymbol{{b}}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\:\:\left(\frac{\mathrm{cos}\:^{\mathrm{2}} \theta}{{a}^{\mathrm{2}} }+\frac{\mathrm{sin}\:^{\mathrm{2}} \theta}{{b}^{\mathrm{2}} }\right){x}^{\mathrm{2}} +\left(\frac{\mathrm{sin}\:^{\mathrm{2}} \theta}{{a}^{\mathrm{2}} }+\frac{\mathrm{cos}\:^{\mathrm{2}} \theta}{{b}^{\mathrm{2}} }\right){y}^{\mathrm{2}} + \\ $$$$\left(\mathrm{2sin}\:\theta\:\mathrm{cos}\:\theta\right)\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }−\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\right){xy}+…=\mathrm{1} \\ $$$${here}\:{in}\:{your}\:{question} \\ $$$${coeff}.\:{of}\:{x}^{\mathrm{2}} =\:{coeff}.\:{of}\:{y}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\mathrm{cos}\:^{\mathrm{2}} \theta\:=\mathrm{sin}\:^{\mathrm{2}} \theta\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{coeff}.\:{of}\:{xy}}{{coeff}.\:{of}\:{x}^{\mathrm{2}} \:{or}\:{y}^{\mathrm{2}} }\:=\frac{\mathrm{2}}{\mathrm{7}} \\ $$$$\Rightarrow\:\:\:\frac{\left(\mathrm{2sin}\:\theta\:\mathrm{cos}\:\theta\right)\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }−\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\right)}{\mathrm{sin}\:^{\mathrm{2}} \theta\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\right)}\:=\frac{\mathrm{2}}{\mathrm{7}} \\ $$$${with}\:\:\mathrm{tan}\:\theta\:=\mathrm{1}\:,\:{we}\:{have} \\ $$$$\:\:\:\:\:\:\frac{\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }−\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\right)}{\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\right)}\:=\:\frac{\mathrm{2}}{\mathrm{7}} \\ $$$$\Rightarrow\:\:\:\:\:\:\:\:\frac{\mathrm{6}}{{a}^{\mathrm{2}} }=\frac{\mathrm{8}}{{b}^{\mathrm{2}} }\:\:\:{or}\:\:\:\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\:=\:\frac{\mathrm{4}}{\mathrm{3}}\:>\:\mathrm{1} \\ $$$${So}\:\:\:\:{e}^{\mathrm{2}} \:=\mathrm{1}−\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\:=\:\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}\:=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${Hence}\:\:\:\boldsymbol{{e}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:. \\ $$
Commented by math solver last updated on 10/Feb/18

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by ajfour last updated on 09/Feb/18
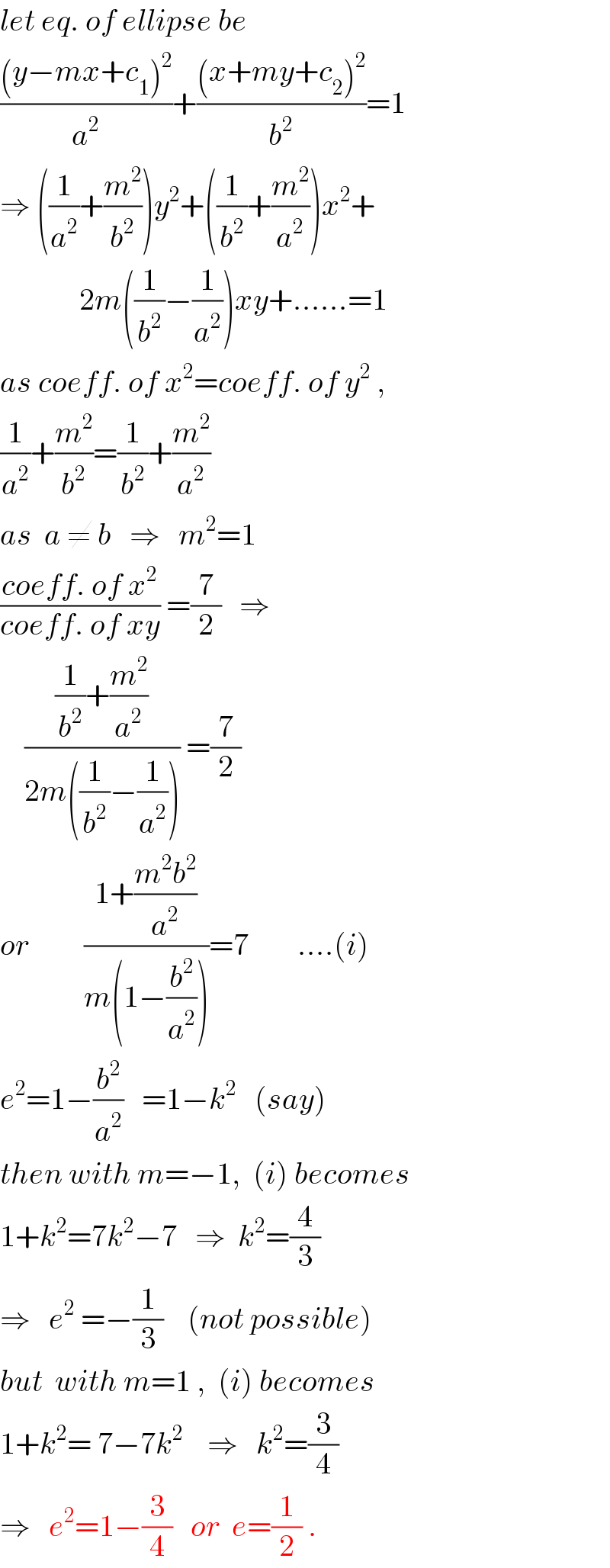
$${let}\:{eq}.\:{of}\:{ellipse}\:{be} \\ $$$$\frac{\left({y}−{mx}+{c}_{\mathrm{1}} \right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left({x}+{my}+{c}_{\mathrm{2}} \right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow\:\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{{m}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\right){y}^{\mathrm{2}} +\left(\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{{m}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right){x}^{\mathrm{2}} + \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}{m}\left(\frac{\mathrm{1}}{{b}^{\mathrm{2}} }−\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\right){xy}+……=\mathrm{1} \\ $$$${as}\:{coeff}.\:{of}\:{x}^{\mathrm{2}} ={coeff}.\:{of}\:{y}^{\mathrm{2}} \:,\: \\ $$$$\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{{m}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{{m}^{\mathrm{2}} }{{a}^{\mathrm{2}} } \\ $$$${as}\:\:{a}\:\neq\:{b}\:\:\:\Rightarrow\:\:\:{m}^{\mathrm{2}} =\mathrm{1} \\ $$$$\frac{{coeff}.\:{of}\:{x}^{\mathrm{2}} }{{coeff}.\:{of}\:{xy}}\:=\frac{\mathrm{7}}{\mathrm{2}}\:\:\:\Rightarrow \\ $$$$\:\:\:\:\frac{\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{{m}^{\mathrm{2}} }{{a}^{\mathrm{2}} }}{\mathrm{2}{m}\left(\frac{\mathrm{1}}{{b}^{\mathrm{2}} }−\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\right)}\:=\frac{\mathrm{7}}{\mathrm{2}}\:\:\:\:\:\: \\ $$$${or}\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}+\frac{{m}^{\mathrm{2}} {b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }}{{m}\left(\mathrm{1}−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)}=\mathrm{7}\:\:\:\:\:\:\:\:….\left({i}\right) \\ $$$${e}^{\mathrm{2}} =\mathrm{1}−\frac{{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\:\:\:=\mathrm{1}−{k}^{\mathrm{2}} \:\:\:\left({say}\right) \\ $$$${then}\:{with}\:{m}=−\mathrm{1},\:\:\left({i}\right)\:{becomes} \\ $$$$\mathrm{1}+{k}^{\mathrm{2}} =\mathrm{7}{k}^{\mathrm{2}} −\mathrm{7}\:\:\:\Rightarrow\:\:{k}^{\mathrm{2}} =\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\Rightarrow\:\:\:{e}^{\mathrm{2}} \:=−\frac{\mathrm{1}}{\mathrm{3}}\:\:\:\:\left({not}\:{possible}\right) \\ $$$${but}\:\:{with}\:{m}=\mathrm{1}\:,\:\:\left({i}\right)\:{becomes} \\ $$$$\mathrm{1}+{k}^{\mathrm{2}} =\:\mathrm{7}−\mathrm{7}{k}^{\mathrm{2}} \:\:\:\:\Rightarrow\:\:\:{k}^{\mathrm{2}} =\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow\:\:\:{e}^{\mathrm{2}} =\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}\:\:\:{or}\:\:{e}=\frac{\mathrm{1}}{\mathrm{2}}\:. \\ $$
